题目内容
7.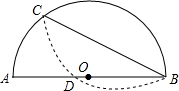 以半圆的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若tanB=$\frac{1}{2}$,且AD=4,则AB=10.
以半圆的一条弦BC(非直径)为对称轴将弧BC折叠后与直径AB交于点D,若tanB=$\frac{1}{2}$,且AD=4,则AB=10.
分析 作线段AB关于直线BC的对称线段BA′,交⊙O于D′,连接AC、CA′,设AC=a,BC=2a,则AB=$\sqrt{5}$a,由A′C•A′A=A′D′•A′B,列出方程解决.
解答 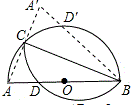 解:作线段AB关于直线BC的对称线段BA′,交⊙O于D′,连接AC、CA′.
解:作线段AB关于直线BC的对称线段BA′,交⊙O于D′,连接AC、CA′.
∵AB是直径,
∴∠ACB=∠BCA′=90°,
∴A、C、A′共线,
根据对称性可知:AD=A′D=4,
∵tan∠ABC=$\frac{AC}{BC}$=$\frac{1}{2}$,设AC=a,BC=2a,则AB=$\sqrt{5}$a,
由A′C•A′A=A′D′•A′B,
∴a•2a=4$•\sqrt{5}$a,
∴a=2$\sqrt{5}$.
AB=$\sqrt{5}$$•2\sqrt{5}$=10.
故答案为10.
点评 本题考查翻折变换、相交弦定理,解题的关键是作线段AB关于直线BC的对称线段BA′,转化为相交弦定理解决问题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
17. 如右图,若AB∥CD,∠1=50°,则∠2的度数是( )
如右图,若AB∥CD,∠1=50°,则∠2的度数是( )
 如右图,若AB∥CD,∠1=50°,则∠2的度数是( )
如右图,若AB∥CD,∠1=50°,则∠2的度数是( )| A. | 50° | B. | 130° | C. | 40° | D. | 145° |
16. 如图所示,与∠B构成同位角的共有( )
如图所示,与∠B构成同位角的共有( )
 如图所示,与∠B构成同位角的共有( )
如图所示,与∠B构成同位角的共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |