题目内容
8.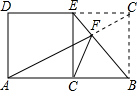 如图所示,在矩形ABCD中,∠DAC=65°,点E是CD上一点,BE交AC于点F,将△BCE沿BE折叠,点C恰好落在AB边上的点C′处,则∠AFC′=40°.
如图所示,在矩形ABCD中,∠DAC=65°,点E是CD上一点,BE交AC于点F,将△BCE沿BE折叠,点C恰好落在AB边上的点C′处,则∠AFC′=40°.
分析 根据直角三角形两锐角互余求出∠ACD,再根据翻折变换的性质判断出四边形BCEC′是正方形,根据正方形的性质可得∠BEC=45°,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BFC,再根据翻折变换的性质可得∠BFC′=∠BFC,然后根据平角等于180°列式计算即可得解.
解答 解:∵矩形ABCD,∠DAC=65°,
∴∠ACD=90°-∠DAC=90°-65°=25°,
∵△BCE沿BE折叠,点C恰好落在AB边上的点C′处,
∴四边形BCEC′是正方形,
∴∠BEC=45°,
由三角形的外角性质,∠BFC=∠BEC+∠ACD=45°+25°=70°,
由翻折的性质得,∠BFC′=∠BFC=70°,
∴∠AFC′=180°-∠BFC-∠BFC′=180°-70°-70°=40°.
故答案为:40°.
点评 本题考查的是翻折变换,正方形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
18.某房地产开发公司计划建A、B两种户型的住房共80套,且A户型不超过50套.已知该公司用于本次建房的资金不超过2096万元.两种户型的建房成本和售价如下表:
(1)试求该公司对建这两种户型住房套数的选定将有哪几种方案;
(2)试问该公司采取(1)中哪种方案建房,才能使获得的利润最大?最大利润为多少万元?
| 户型 | A | B |
| 成本(万元/套) | 25 | 28 |
| 售价(万元/套) | 30 | 34 |
(2)试问该公司采取(1)中哪种方案建房,才能使获得的利润最大?最大利润为多少万元?
3.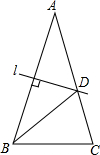 如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )
如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )
 如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )
如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 75° |
20.下列关于图形对称性的命题,正确的是( )
| A. | 圆既是轴对称图形,又是中心对称图形 | |
| B. | 正三角形既是轴对称图形,又是中心对称图形 | |
| C. | 线段是轴对称图形,但不是中心对称图形 | |
| D. | 菱形是中心对称图形,但不是轴对称图形 |
18.一元二次方程2x2-5x-2=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
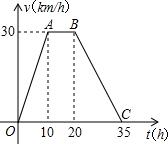 据某气象站观察和预测:发生于甲地的热带风暴正向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.
据某气象站观察和预测:发生于甲地的热带风暴正向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.