题目内容
17.下列各式:$\frac{1}{8}(1-x)$,$\frac{4x}{π-3}$,$\frac{{{x^2}-{y^2}}}{2}$,$\frac{1}{x}+x$,$\frac{{5{x^2}}}{x}$,其中分式共有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 依据分式的定义回答即可.
解答 解:$\frac{1}{8}(1-x)$,分母中不含字母,不是分式;
$\frac{4x}{π-3}$π是数字,不是字母,故分母中不含字母,不是分式;
$\frac{{{x^2}-{y^2}}}{2}$分母中不含字母,不是分式;
$\frac{1}{x}+x$的分母中含有字母,是分式;
$\frac{{5{x^2}}}{x}$的分母中含有字母,是分式.
故选:A.
点评 本题主要考查的是分式的定义,掌握分式的定义是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
2.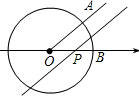 如图,已知⊙O圆心是数轴原点,半径为1,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
如图,已知⊙O圆心是数轴原点,半径为1,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
 如图,已知⊙O圆心是数轴原点,半径为1,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
如图,已知⊙O圆心是数轴原点,半径为1,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )| A. | -1≤x≤1 | B. | -$\sqrt{2}$≤x≤$\sqrt{2}$ | C. | 0≤x≤$\sqrt{2}$ | D. | x>$\sqrt{2}$ |
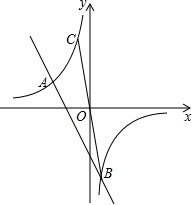 如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A(-3,2)和点B(1,m),连接BO并延长与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点C.
如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A(-3,2)和点B(1,m),连接BO并延长与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点C.
 利用“等边对等角”
利用“等边对等角”