题目内容
11. 如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是( )
如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是( )| A. | AB=AD | B. | AC=BD | C. | AD=BC | D. | AB=CD |
分析 由点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,根据三角形中位线的性质,可得EF=GH=$\frac{1}{2}$AB,EH=FG=$\frac{1}{2}$CD,又由当EF=FG=GH=EH时,四边形EFGH是菱形,即可求得答案.
解答 解:∵点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,
∴EF=GH=$\frac{1}{2}$AB,EH=FG=$\frac{1}{2}$CD,
∵当EF=FG=GH=EH时,四边形EFGH是菱形,
∴当AB=CD时,四边形EFGH是菱形.
故选:D.
点评 此题考查了中点四边形的性质、菱形的判定以及三角形中位线的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
2.若$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{2x+y=m}\\{x-ny=3}\end{array}\right.$的解,则m,n的值为( )
| A. | 3,1 | B. | 3,-1 | C. | -3,1 | D. | -3,-1 |
16.如图1,平行四边形纸片ABCD的面积为60,沿对角线AC,BD将其裁剪成四个三角形纸片,将纸片△AOD翻转后,与纸片△COB拼接成如图2所示的四边形(点A与点C,点D与点B重合),则拼接后的四边形的两条对角钱之积为( )


| A. | 30 | B. | 40 | C. | 50 | D. | 60 |
3.事件“反比例函数y=$\frac{k}{x}$(k>0)经过点(0,3)”的概率是( )
| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{1}{k}$ | D. | 1 |
20. 如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
 如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )| A. | 42° | B. | 44° | C. | 46° | D. | 48° |
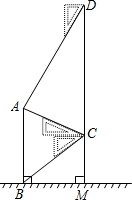 如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).
如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).