题目内容
10.解不等式组$\left\{\begin{array}{l}{2x-6<6-2x}\\{4x+2>3+x}\end{array}\right.$.分析 首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:$\left\{\begin{array}{l}{2x-6<6-2x…①}\\{4x+2>3+x…②}\end{array}\right.$,
解①得x<3,
解②得x>$\frac{1}{3}$.
则不等式组的解集是:$\frac{1}{3}$<x<3.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
18.把抛物线y=-2x2+1向左平移1个单位,然后向上平移3个单位,则平移后抛物线的顶点坐标是( )
| A. | (-1,-4) | B. | (-1,4) | C. | (1,-4) | D. | (1,4) |
5.若$\sqrt{{-(1-a)}^{2}}$有意义,则满足条件的a的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.若$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{2x+y=m}\\{x-ny=3}\end{array}\right.$的解,则m,n的值为( )
| A. | 3,1 | B. | 3,-1 | C. | -3,1 | D. | -3,-1 |
20. 如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
 如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )| A. | 42° | B. | 44° | C. | 46° | D. | 48° |

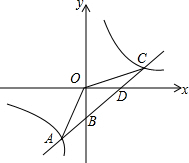 如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.