题目内容
15.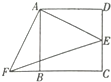 如图,四边形ABCD是正方形,F分别是DC和BC的延长线上的点,且DE=BF,连结AE,AF,EF.
如图,四边形ABCD是正方形,F分别是DC和BC的延长线上的点,且DE=BF,连结AE,AF,EF.(1)求证:△ADE≌△ABF;
(2)若BC=8,DE=6,求EF的长.
分析 (1)根据正方形性质得出∠ADE=∠ABC=90°=∠ABF,根据SAS推出全等即可;
(2)根据全等三角形的性质求出BF=6,求出CF和CE,根据勾股定理求出即可.
解答 (1)证明:∵四边形ABCD是正方形,
∴∠ADE=∠ABC=90°=∠ABF,
在△ADE和△ABF中,
$\left\{\begin{array}{l}{AD=AB}\\{∠D=∠ABF}\\{DE=BF}\end{array}\right.$,
∴△ADE≌△ABF(SAS);
(2)解:∵△ADE≌△ABF,DE=6,
∴BF=DE=6,
∵BC=DC=8,
∴CE=8-6=2,CF=8+6=14,
在Rt△FCE中,EF=$\sqrt{C{F}^{2}+C{E}^{2}}$=$\sqrt{1{4}^{2}+{2}^{2}}$=10$\sqrt{2}$.
点评 本题考查了正方形的性质,全等三角形的性质和判定,勾股定理的应用,能求出△ADE≌△ABF是解此题的关键,注意:全等三角形的对应边相等.

练习册系列答案
相关题目
5.若$\sqrt{{-(1-a)}^{2}}$有意义,则满足条件的a的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.事件“反比例函数y=$\frac{k}{x}$(k>0)经过点(0,3)”的概率是( )
| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{1}{k}$ | D. | 1 |
20. 如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
 如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )
如图,直线AB∥CD,∠1=136°,∠E为直角,则∠C等于( )| A. | 42° | B. | 44° | C. | 46° | D. | 48° |
7.下列命题中,是真命题的是( )
| A. | 相等的角是对顶角 | B. | 垂线段最短 | ||
| C. | $\sqrt{81}$的平方根是±9 | D. | 无限小数都是无理数 |
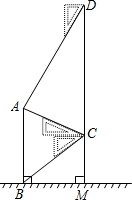 如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).
如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73). 如图,直线y=kx过点A(1,2),直线y=-2x-5与x轴交于B点,直线y=kx与直线y=-2x-5交于C点,
如图,直线y=kx过点A(1,2),直线y=-2x-5与x轴交于B点,直线y=kx与直线y=-2x-5交于C点,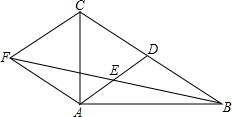 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.