题目内容
19. 背景材料:近年来由于世界各国大力发展海洋经济、加强海洋能力开发,海洋争端也呈上升趋势.为增强海洋执法能力、维护海洋领土,近期我国多个部门联合进行护航、护渔演习.
背景材料:近年来由于世界各国大力发展海洋经济、加强海洋能力开发,海洋争端也呈上升趋势.为增强海洋执法能力、维护海洋领土,近期我国多个部门联合进行护航、护渔演习.解决问题:
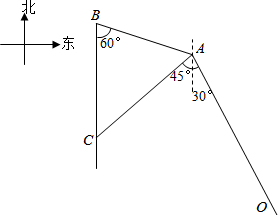
(1)如图,我国渔船(C)在钓鱼岛海域正被某国不明船只袭扰,“中国海政310”船(A)接到陆地指挥中心(B)护渔命令时,渔船(C)位于陆地指挥中心正南方向,位于“中国海政310”船西南方向,“中国海政310”船位于陆地指挥中心南偏东60°方向,AB=$\frac{{140\sqrt{6}}}{3}$海里,“中国海政310”船最大航速为20海里/小时.根据以上信息,请你求出“中国海政310”船赶往渔船所在位置进行护渔至少需要多长时间?
(2)如果(1)中条件不变,此时位于“中国海政310”船(A)南偏东30°海域有一只某国军舰(O),AO=560$\sqrt{2}$海里,其火力打击范围是500海里,如果渔船沿着正南方向继续航行,是否会驶进这只军舰的打击范围?
分析 (1)首先过点A作AD⊥BC于点D,利用锐角三角函数关系求出AD,AC的长即可得出答案;
(2)首先延长BC,过点O作OE⊥BC的延长线于点E,过点A作AF⊥OE于点F,得出AD的长,进而得出OE的长即可得出答案.
解答 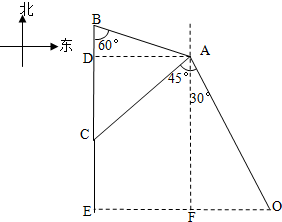 解:(1)过点A作AD⊥BC于点D
解:(1)过点A作AD⊥BC于点D
∵AB=$\frac{{140\sqrt{6}}}{3}$,∠B=60°,
∴sinB=$\frac{AD}{AB}$,
∴AD=AB•sin60°=$\frac{{140\sqrt{6}}}{3}$•$\frac{{\sqrt{3}}}{2}$=70$\sqrt{2}$(海里),
在Rt△ADC中,AD=70$\sqrt{2}$,∠C=45°,
∴AC=70$\sqrt{2}$•$\sqrt{2}$=140(海里),
∴“中国海政310”船赶往出事点至少需:140÷20=7(小时);
(2)延长BC,过点O作OE⊥BC的延长线于点E,过点A作AF⊥OE于点F,
∵AD⊥BC,∴四边形ADEF是矩形,∴AD=EF=70$\sqrt{2}$,
在Rt△AFO中,∵AO=560$\sqrt{2}$,∠OAF=30°,
∴OF=$\frac{1}{2}$OA=280$\sqrt{2}$(海里),
∴OE=280$\sqrt{2}$+70$\sqrt{2}$=350$\sqrt{2}$<500,
所以如果渔船沿着正南方向继续航行,会驶进这只军舰的打击范围.
点评 此题主要考查了解直角三角形的应用,根据题意正确构造直角三角形是解题关键.

练习册系列答案
相关题目
9.如果两个圆的半径分别为5和3,圆心距为4,那么两圆的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 外离 | D. | 内含 |
14.下列说法正确的是( )
| A. | 如果a>b>0,那么$\frac{1}{a}>\frac{1}{b}$ | |
| B. | 函数y=$\frac{{\sqrt{x+1}}}{x}$自变量的取值范围是x≥-1 | |
| C. | 2<$\sqrt{5}$<3 | |
| D. | 若a≠0,则$\frac{{\sqrt{a^2}}}{a}$=1 |
4.方程x2+2x-3=0的解是( )
| A. | 1 | B. | 3 | C. | -3 | D. | 1或-3 |
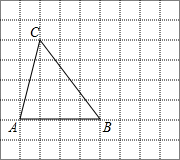 作图题:在方格纸中,将△ABC向右平移4个单位得到△A1B1C1
作图题:在方格纸中,将△ABC向右平移4个单位得到△A1B1C1