题目内容
6.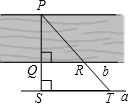 如图,为了估计荆河的宽度,在荆河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS=60m,ST=120m,QR=80m,则荆河的宽度PQ为( )
如图,为了估计荆河的宽度,在荆河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS=60m,ST=120m,QR=80m,则荆河的宽度PQ为( )| A. | 40m | B. | 120m | C. | 60m | D. | 180m |
分析 由题意可知:QR∥ST,所以△PQR∽△PST,由相似三角形的性质可知$\frac{PQ}{PS}$=$\frac{QR}{ST}$,列出方程即可求出PQ的长度
解答 解:由题意可知:QR∥ST,
∴△PQR∽△PST,
∴$\frac{PQ}{PS}$=$\frac{QR}{ST}$
设PQ=x,
∴$\frac{x}{x+60}=\frac{80}{120}$
解得:x=120
故PQ=120m
故选(B)
点评 本题考查相似三角形的应用,解题的关键是利用相似三角形的对应边的比相等求出PQ的长度,本题属于基础题型.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
14.从下列四张卡片中任取一张,卡片上的图形既是轴对称又是中心对称图形的概率是( )


| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
15.甲、乙两名队员参加射击训练,成绩分布被制成下列两个统计图:
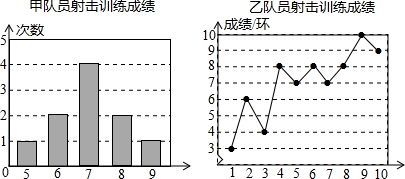
根据以上信息,整理分析数据如下:
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?

根据以上信息,整理分析数据如下:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | 7 | b | 7 | c |
| 乙 | a | 7.5 | 8 | 4.2 |
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
 如图,△ABC的顶点坐标分别为A(4,5),B(2,3),C(5,1).
如图,△ABC的顶点坐标分别为A(4,5),B(2,3),C(5,1).