题目内容
14.从下列四张卡片中任取一张,卡片上的图形既是轴对称又是中心对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
分析 根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数.二者的比值就是其发生的概率的大小.
解答 解:∵四张卡片中任取一张既是轴对称又是中心对称图形的有2张,
∴卡片上的图形既是轴对称又是中心对称图形的概率是$\frac{2}{4}$=$\frac{1}{2}$,
故选:B.
点评 本题考查轴对称图形、中心对称图形及概率公式,其中涉及的轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称;中心对称图形的概念:是指这个图形绕着对称中心旋转180°后仍然能和这个图形重合的图形;简易概率求法公式:P(A)=$\frac{m}{n}$,其中0≤P(A)≤1.

练习册系列答案
相关题目
6.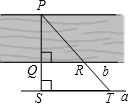 如图,为了估计荆河的宽度,在荆河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS=60m,ST=120m,QR=80m,则荆河的宽度PQ为( )
如图,为了估计荆河的宽度,在荆河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS=60m,ST=120m,QR=80m,则荆河的宽度PQ为( )
 如图,为了估计荆河的宽度,在荆河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS=60m,ST=120m,QR=80m,则荆河的宽度PQ为( )
如图,为了估计荆河的宽度,在荆河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS=60m,ST=120m,QR=80m,则荆河的宽度PQ为( )| A. | 40m | B. | 120m | C. | 60m | D. | 180m |
4.一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )
| A. | 至少有1个球是白球 | B. | 至少有1个球是黑球 | ||
| C. | 至少有2个球是黑球 | D. | 至少有2个球是白球 |
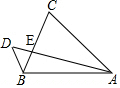 如图.在△ABC中,AB=AC,D为△ABC外一点,连结AD,交BC于点E,连结DB,若∠C=∠D,AE=8,DE=2.求AC的长.
如图.在△ABC中,AB=AC,D为△ABC外一点,连结AD,交BC于点E,连结DB,若∠C=∠D,AE=8,DE=2.求AC的长.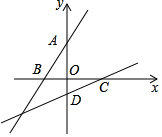 如图,已知A、B、C、D是平面直角坐标系中坐标轴上的点,且△AOB≌△COD,设直线AB的表达式为y1=ax+b,直线CD的表达式为y2=mx+n,则am=1.
如图,已知A、B、C、D是平面直角坐标系中坐标轴上的点,且△AOB≌△COD,设直线AB的表达式为y1=ax+b,直线CD的表达式为y2=mx+n,则am=1. 如图,∠AOB=90°,OE、OF分别平分∠BOC、∠AOB,如果∠EOF=60°,求∠AOC的度数.
如图,∠AOB=90°,OE、OF分别平分∠BOC、∠AOB,如果∠EOF=60°,求∠AOC的度数. 如图所示,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,若∠AOD=96°,∠MON=68°,求∠BOC的大小.
如图所示,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,若∠AOD=96°,∠MON=68°,求∠BOC的大小.