题目内容
9. 如图,在△ABC中,AB=AC=6,BC=4,⊙B与边AB相交于点D,与边BC相交于点E,设⊙B的半径为x.
如图,在△ABC中,AB=AC=6,BC=4,⊙B与边AB相交于点D,与边BC相交于点E,设⊙B的半径为x.(1)当⊙B与直线AC相切时,求x的值;
(2)设DC的长为y,求y关于x的函数解析式,并写出定义域;
(3)若以AC为直径的⊙P经过点E,求⊙P与⊙B公共弦的长.
分析 (1)根据勾股定理,求出AG,再由割线定理,求出BH即可;
(2)由相似得出比例式,表示出DF,CF,由勾股定理建立函数关系式;
(3)根据圆的性质求出BE,CE,再用△BQP∽△BGE,求出EG即可,
解答 解:(1)如图1,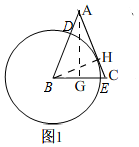
作AG⊥BC,BH⊥AC,
∵AB=AC,AG⊥BC,
∴BG=CG=2,
∴AG=$\sqrt{A{C}^{2}-C{G}^{2}}$=4$\sqrt{2}$,
∵AG×BC=BH×AC,
∴BH=$\frac{AG×BC}{AC}$=$\frac{8\sqrt{2}}{3}$,
∴当⊙B与直线AC相切时,x=$\frac{8\sqrt{2}}{3}$;
(2)如图2,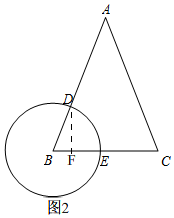
作DF⊥BC,
∴DF∥AG,
∴$\frac{BD}{AB}=\frac{DF}{AG}$,
∴$\frac{x}{6}=\frac{DF}{4\sqrt{2}}$,
∴DF=$\frac{2\sqrt{2}}{3}$x,
∴CF=4-$\frac{1}{3}$x,
在Rt△CFD中,CD2=DE2+CF2,
∴y=$\sqrt{(4-\frac{1}{3}x)^{2}+({\frac{2\sqrt{2}}{3}x)}^{2}}$=$\sqrt{x2-\frac{8}{3}x+16}$(0<x≤4),
(3)①如图3,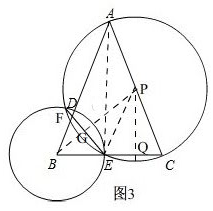
作PQ⊥BC,连接PE,AE,
∵EF是⊙B,⊙P的公共弦,
∵⊙P经过点E,
∴PA=PE=PC,
∴AE⊥BC,
∵AC=AB,
∴BE=CE=2,
∵PQ∥AE,且P是AC中点,
∴PQ=$\frac{1}{2}$AE=2$\sqrt{2}$,CP=3,
∴CQ=1,BQ=3,
∴BP=$\sqrt{17}$,
∵EF是⊙P,⊙B的公共弦,
∴∠BGE=90°=∠BQP(两圆的连心线垂直于公共弦)
∵∠EBG=∠PBQ
∴△BQP∽△BGE,
∴$\frac{EG}{PQ}=\frac{BE}{BP}$,
∴$\frac{EG}{2\sqrt{2}}=\frac{2}{\sqrt{17}}$,
∴EG=$\frac{4\sqrt{34}}{17}$,
∴EF=$\frac{8\sqrt{34}}{17}$;
②当点E,与点C重合时,EF=$\frac{16\sqrt{34}}{17}$.
点评 此题是圆的综合题,主要考查了勾股定理,切线的判定,相似三角形的判定和性质,解本题的关键是用圆中角的关系,判断三角形相似.

 名校课堂系列答案
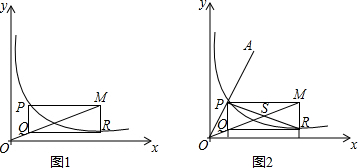
名校课堂系列答案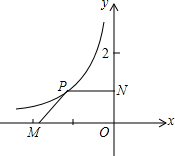 如图,平面直角坐标系中,点M是x轴负半轴上一定点,点P是函数y=-$\frac{1}{x}$,(x<0)上一动点,PN⊥y轴于点N,当点P的横坐标在逐渐增大时,四边形PMON的面积将会( )
如图,平面直角坐标系中,点M是x轴负半轴上一定点,点P是函数y=-$\frac{1}{x}$,(x<0)上一动点,PN⊥y轴于点N,当点P的横坐标在逐渐增大时,四边形PMON的面积将会( )| A. | 逐渐增大 | B. | 始终不变 | C. | 逐渐减小 | D. | 先增后减 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
| 衡量指标 | 小敏 | 小芳 | 小聪 | 小明 |
| 平均数 | 90 | 85 | 90 | 85 |
| 方差 | 3 | 3 | 10 | 12 |
| A. | 小明 | B. | 小芳 | C. | 小聪 | D. | 小敏 |
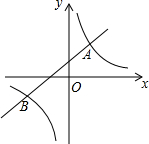 如图,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)相交于A(1,2),B(n,-1)两点.
如图,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)相交于A(1,2),B(n,-1)两点.