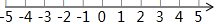题目内容
8.定义:对角线互相垂直的凸四边形叫做“垂直四边形”.(1)理解:
如图1,已知四边形ABCD是“垂直四边形”,对角线AC,BD交于点O,AC=8,BD=7,求四边形ABCD的面积.
(2)探究:
小明对“垂直四边形”ABCD(如图1)进行了深入探究,发现其一组对边的平方和等于另一组对边的平方和.即AB2+CD2=AD2+BC2.你认为他的发现正确吗?试说明理由.
(3)应用:
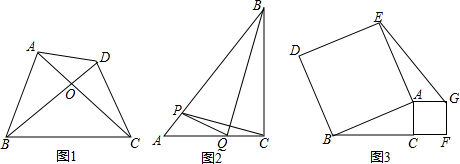
①如图2,在△ABC中,∠ACB=90°,AC=6,BC=8,动点P从点A出发沿AB方向以每秒5个单位的速度向点B匀速运动,同时动点Q从点C出发沿CA方向以每秒6个单位的速度向点A匀速运动,运动时间为t秒(0<t<1),连结CP,BQ,PQ.当四边形BCQP是“垂直四边形”时,求t的值.
②如图3,在△ABC中,∠ACB=90°,AB=3AC,分别以AB,AC为边向外作正方形ABDE和正方形ACFG,连结EG.请直接写出线段EG与BC之间的数量关系.
分析 (1)根据三角形的面积公式计算;
(2)根据勾股定理列出算式,比较即可;
(3)①作PD⊥AC于D,根据勾股定理求出AB,根据相似三角形的性质用t表示出AP、CQ、AD、PD,根据垂直四边形的性质列出方程,解方程即可;
②作CP⊥AB于P,GH⊥EA交EA的延长线于H,证明△CAP≌△GAH,得到PC=GH,设CA=x,根据勾股定理分别用x表示出BC和EG,计算即可.
解答 解:(1)理解:
四边形ABCD的面积=$\frac{1}{2}$×BD×AO$+\frac{1}{2}×$BD×OC
=$\frac{1}{2}×$BD×AC
=28;
(2)探究:
∵AC⊥BD,
∴AB2=OA2+OB2,
CD2=OD2+OC2,
AD2=OA2+OD2,
BC2=OC2+OB2,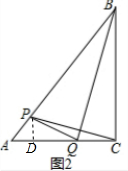
∴AB2+CD2=OA2+OB2+OD2+OC2,
AD2+BC2=OA2+OB2+OD2+OC2,
∴AB2+CD2=AD2+BC2;
(3)应用:
①如图2,作PD⊥AC于D,
∵∠ACB=90°,AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
∵PD∥BC,
∴$\frac{AD}{AC}$=$\frac{PD}{BC}$=$\frac{AP}{AB}$,
由题意得,AP=5t,CQ=6t,
则$\frac{AD}{6}$=$\frac{PD}{8}$=$\frac{5t}{10}$,
解得,AD=3t,PD=4t,
∵四边形BCQP是“垂直四边形”,
∴BP2+CQ2=PQ2+BC2,即(10-5t)2+(6t)2=(4t)2+(6-9t)2+82,
解得,t=$\frac{2}{9}$,
当t=$\frac{2}{9}$时,四边形BCQP是“垂直四边形”;
②如图3,作CP⊥AB于P,GH⊥EA交EA的延长线于H,
∵∠EAG+∠BAC=360°-90°-90°=180°,
∠EAG+∠GAH=180°,
∴∠BAC=∠GAH,
在△CAP和△GAH中,
$\left\{\begin{array}{l}{∠CAP=∠GAH}\\{∠APC=∠AHG}\\{AC=AG}\end{array}\right.$,
∴△CAP≌△GAH,
∴PC=GH,
设CA=x,则AB=3x,
由勾股定理得BC=2$\sqrt{2}$x,
则PC=$\frac{AC×BC}{AB}$=$\frac{2\sqrt{2}}{3}$x,
∴AH=$\frac{1}{3}$x,
由勾股定理得,EG=$\sqrt{E{H}^{2}+G{H}^{2}}$=2$\sqrt{3}$x,
∴$\frac{EG}{BC}$=$\frac{2\sqrt{3}x}{2\sqrt{2}x}$=$\frac{\sqrt{6}}{2}$,
∴EG=$\frac{\sqrt{6}}{2}$BC.
点评 本题考查的是垂直四边形的概念和性质、相似三角形的判定和性质以及勾股定理的应用,正确理解垂直四边形的定义、灵活运用勾股定理是解题的关键.

| A. | -1-$\sqrt{2}$ | B. | 1-$\sqrt{2}$ | C. | -2+$\sqrt{2}$ | D. | -2-$\sqrt{2}$ |
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 3 | 4 | 3 | 0 | -5 | … |
| A. | x1=2,x2=-2 | B. | x1=2,x2=-3 | C. | x1=2,x2=-4 | D. | x1=2,x2=-5 |
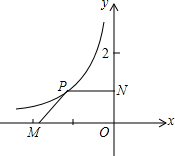 如图,平面直角坐标系中,点M是x轴负半轴上一定点,点P是函数y=-$\frac{1}{x}$,(x<0)上一动点,PN⊥y轴于点N,当点P的横坐标在逐渐增大时,四边形PMON的面积将会( )
如图,平面直角坐标系中,点M是x轴负半轴上一定点,点P是函数y=-$\frac{1}{x}$,(x<0)上一动点,PN⊥y轴于点N,当点P的横坐标在逐渐增大时,四边形PMON的面积将会( )| A. | 逐渐增大 | B. | 始终不变 | C. | 逐渐减小 | D. | 先增后减 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
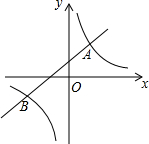 如图,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)相交于A(1,2),B(n,-1)两点.
如图,直线y=kx+b(k≠0)与双曲线y=$\frac{m}{x}$(m≠0)相交于A(1,2),B(n,-1)两点.