题目内容
6．我们知道直线y=kx+3一定经过点（0，3），同样直线y=（k-1）x+3k+2一定经过的点为（-3，5）．分析 将直线方程转化为y=k（x+3）+（-x+2）的形式，问题转化为：无论k取何值，该函数都经过一定点．
解答 解：由直线y=（k-1）x+3k+2得
y=k（x+3）+（-x+2），
∴x+3=0，
∴x=-3，
代入y=k（x+3）+（-x+2），得y=5，
∴直线一定经过点（-3，5）．
故答案是：（-3，5）．
点评 此题主要考查了一次函数图象上点的坐标特征，只要点在函数的图象上，则一定满足函数的解析式．反之，只要满足函数解析式的点就一定在函数的图象上．
练习册系列答案
阅读快车系列答案
相关题目
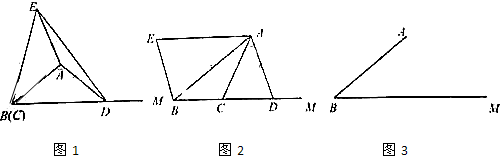
16．
规定：如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点B的极坐标应记为（ ）
规定：如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点B的极坐标应记为（ ）| A． | （2$\sqrt{3}$，30°） | B． | （60°，2$\sqrt{3}$） | C． | （30°，4） | D． | （30°，2$\sqrt{3}$） |
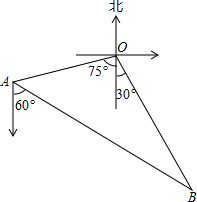如图，编号为2307和2308的两艘海监船同时从港口O出发外出某岛海域巡航，2307海监船沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行，2308海监船沿南偏东30°方向以每小时15海里的速度航行，航行1小时后，2307海监船在A处收到消息，2308海监船附近发现疑似敌舰，于是2307海监船迅速改变航向和速度，以匀速沿南偏东60°方向追赶2308海监船，正好在B处追上，2307海监船追赶2308海监船的速度为多少海里/时？
如图，AD⊥BD，AC⊥BC，AD与BC交于点O，AD=BC．
15．制动距离是汽车处于某一时速的情况下，从开始刹车制动到汽车完全静止时，车辆所开过的路程，对某辆汽车进行测试时，汽车的行驶速度与汽车的制动距离的数据如表所示
（1）该汽车的制动距离s是变量还是常量？
（2）若s是v的一次函数，求s关于v的函数解析式．
| 汽车行驶速度v（千米/小时） | 30 | 40 | 50 | 60 | 70 |
| 制动距离s（米） | 5 | 12 | 19 | 26 | 33 |
（2）若s是v的一次函数，求s关于v的函数解析式．
已知A，B两地公路长300km，甲、乙两车同时从A地出发沿同一公路驶往B地，2小时后，甲车接到电话需返回这条公路上的C处取回货物，于是甲车立即原路返回C地，取了货物又立即赶往B地（取货物的时间忽略不计），结果两车同时到达B地．两车的速度始终保持不变，设两车出发xh后，甲、乙距离A地的距离分别为y1（km）和y2（km），它们的函数图象分别是折线OPQR和线段OR．