题目内容
14.当-1≤x≤2时,二次函数y=x2+2kx+k+1的最小值是-1,则k的值可能是-1,2,3.分析 分类讨论①当x=-1取得最小值.②当x=2取得最小值.③当$\frac{4(k+1)-4{k}^{2}}{4}$=-1.然后画出草图判定是否符合题意即可.
解答 解:∵-1≤x≤2时,二次函数y=x2+2kx+k+1的最小值是-1,
∴最小值可能在x=-1或2时得到,或最小值=$\frac{4ac-{b}^{2}}{4a}$,
①当x=-1取得最小值,1-2k+k+1=-1,k=3,此时对称轴x=-$\frac{2k}{2}$=-3,x=-1时有最小值,所以合题意.
②当x=2取得最小值,4+4k+k+1=-1,k=-$\frac{6}{5}$,x=-1时有最小值,不符合题意.
③当$\frac{4(k+1)-4{k}^{2}}{4}$=-1,k=2或-1,k=2时,对称轴x=2,x=2时有最小值,符合题意,
当k=-1时,对称轴x=-1,x=-1时有最小值,符合题意.
∴k的值可能是-1,2,3,
故答案为-1,2,3.
点评 本题考查二次函数的最值问题、解题的关键是学会分类讨论,注意这个最小值可以在区间的端点x=1或x=3时取得,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.如果关于x的一元二次方程x2-4|a|x+4a2-1=0的一个根是5,则方程的另一个根是( )
| A. | 1 | B. | 5 | C. | 7 | D. | 3或7 |
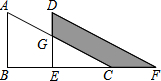 如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$.
如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$.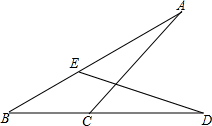 如图,已知AC=DE,AB=BD,求证:BC=BE.
如图,已知AC=DE,AB=BD,求证:BC=BE. 如图,直线y=2x-4分别交坐标轴于A、B两点,交双曲线y=$\frac{k}{x}$(x>0)于C点,且sin∠COB=$\frac{\sqrt{2}}{2}$.
如图,直线y=2x-4分别交坐标轴于A、B两点,交双曲线y=$\frac{k}{x}$(x>0)于C点,且sin∠COB=$\frac{\sqrt{2}}{2}$.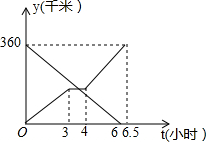 一辆货车从甲地向乙地行驶,一辆小轿车与该货车同时出发,从乙地向甲地行驶,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至甲地,货车与乙地的距离y1(千米)、小轿车与乙地的距离y2(千米)与行驶时间((小时)之间的函数关系的图象如图所示,已知当小轿车行驶2小时时,小轿车与货车相距140千米.
一辆货车从甲地向乙地行驶,一辆小轿车与该货车同时出发,从乙地向甲地行驶,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至甲地,货车与乙地的距离y1(千米)、小轿车与乙地的距离y2(千米)与行驶时间((小时)之间的函数关系的图象如图所示,已知当小轿车行驶2小时时,小轿车与货车相距140千米.