Question

17．已知，AB=5，tan∠ABM=$\frac{3}{4}$，点C、D、E为动点，其中点C、D在射线BM上（点C在点D的左侧），点E和点D分别在射线BA的两侧，且AC=AD，AB=AE，∠CAD=∠BAE．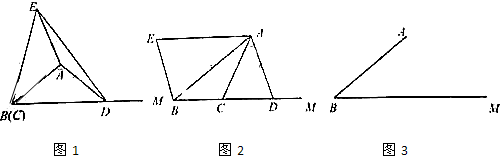

（1）当点C与点B重合时（如图1），联结ED，求ED的长；
（2）当EA∥BM时（如图2），求四边形AEBD的面积；
（3）联结CE，当△ACE是等腰三角形时，求点B、C间的距离．

Answer 1

分析 （1）如图1中，延长BA交DE于F，作AH⊥BD于H，先证明BF⊥DE，EF=DF，再利用△ABH∽△DBF，得$\frac{AH}{DF}$=$\frac{AB}{BD}$，求出DF即可解决问题．
（2）先证明四边形ADBE是平行四边形，根据S_{平行四边形ADBE}=BD•AH，计算即可．
（3）由题意AC≠AE，EC≠AC，只有EA=EC，利用四点共圆先证明四边形ADBE是平行四边形，求出DH、CH即可解决问题．

解答 解：（1）如图1中，延长BA交DE于F，作AH⊥BD于H．

在RT△ABH中，∵∠AHB=90°，
∴sin∠ABH=$\frac{AH}{AB}$=$\frac{3}{5}$，
∴AH=3，BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=4，
∵AB=AD，AH⊥BD，
∴BH=DH=4，
在△ABE 和△ABD中，
$\left\{\begin{array}{l}{AE=AD}\\{∠BAE=∠BAD}\\{AB=AB}\end{array}\right.$，
∴△ABD≌△ABE，
∴BE=BD，∠ABE=∠ABD，
∴BF⊥DE，EF=DF，
∵∠ABH=∠DBF，∠AHB=∠BFD，
∴△ABH∽△DBF，
∴$\frac{AH}{DF}$=$\frac{AB}{BD}$，
∴DF=$\frac{24}{5}$，
∴DE=2DF=$\frac{48}{5}$．
（2）如图2中，作AH⊥BD于H．

∵AC=AD，AB=AE，∠CAD=∠BAE，
∴∠AEB=∠ABE=∠ACD=∠ADC，
∵AE∥BD，
∴∠AEB+∠EBD=180°，
∴∠EBD+∠ADC=180°，
∴EB∥AD，
∵AE∥BD，
∴四边形ADBE是平行四边形，
∴BD=AE=AB=5，AH=3，
∴S_{平行四边形ADBE}=BD•AH=15．
（3）由题意AC≠AE，EC≠AC，只有EA=EC．
如图3中，

∵∠ACD=∠AEB（已证），
∴A、C、B、E四点共圆，
∵AE=EC=AB，
∴$\widehat{EC}$=$\widehat{AB}$，
∴$\widehat{EB}$=$\widehat{AC}$，
∴∠AEC=∠ABC，
∴AE∥BD，
由（2）可知四边形ADBE是平行四边形，
∴AE=BD=AB=5，
∵AH=3，BH=4，
∴DH=BD-BH=1，
∵AC=AD，AH⊥CD，
∴CH=HD=1，
∴BC=BD-CD=3．

点评 本题考查三角形综合题、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识，解题的关键是添加辅助线构造全等三角形，第三个问题的关键是利用四点共圆的性质解决问题，属于中考压轴题．