Question

10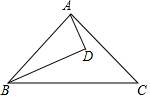．如图，BD是∠ABC的角平分线，AD⊥BD，垂足为D，∠DAC=20°，∠C=15°，则∠BAD=35°．

Answer 1

分析 设∠ABD=α，∠BAD=β，利用三角形内角和定理即可求出列出方程求出α与β的值．

解答 解：设∠ABD=α，∠BAD=β
∵AD⊥BD
∴∠ABD+∠BAD=90°，
即α+β=90°
∵BD是∠ABC得角平分线，
∴∠ABC=2∠ABD=2α，
∵∠ABC+∠BAC+∠C=180
∴2α+β+15°+20°=180°，
∴联立可得$\left\{\begin{array}{l}{α+β=90°}\\{2α+β=145°}\end{array}\right.$
解得：$\left\{\begin{array}{l}{α=55°}\\{β=35°}\end{array}\right.$
∴∠BAD=35°
故答案为：35°

点评 本题考查三角形内角和，解题的关键是根据条件列出关于α与β的方程组，本题属于中等题型．