题目内容
18.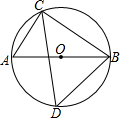 如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )
如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )| A. | CD=(AC+BC)sinθ | B. | CD=(AC+BC)cosθ | ||
| C. | CD=AC•cosθ+BC•sinθ | D. | CD=AC•sinθ+BC•cosθ |
分析 连接AD,作BH⊥CD于H,根据圆周角定理得到∠ACB=∠ADB=90°,根据正弦、余弦的定义求出BD、BH,根据勾股定理求出DH,计算即可.
解答 解: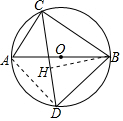 连接AD,作BH⊥CD于H,
连接AD,作BH⊥CD于H,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
∴BD=AB•sin∠BAD=AB•sinθ,
在Rt△ACB中,AC2+BC2=AB2=$\frac{B{D}^{2}}{si{n}^{2}θ}$,
即BD2=AC2sin2θ+BC2sin2θ,
BH=BC•sinθ,CH=BC•cosθ,
DH=$\sqrt{B{D}^{2}-B{H}^{2}}$=AC•sinθ,
∴CD=CH+DH=AC•sinθ+BC•cosθ,
故选:D.
点评 本题考查的是三角形的外接圆和外心的概念和性质,掌握圆周角定理、勾股定理、锐角三角函数的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 如图,AC⊥BC,且BC=6,AC=8,AB=10,则点B到AC的距离是( )
如图,AC⊥BC,且BC=6,AC=8,AB=10,则点B到AC的距离是( )
 如图,AC⊥BC,且BC=6,AC=8,AB=10,则点B到AC的距离是( )
如图,AC⊥BC,且BC=6,AC=8,AB=10,则点B到AC的距离是( )| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
13.已知三角形两边长分别是a,b(b>a),则三角形的周长C应满足( )
| A. | 2b<C<2(a+b) | B. | a+b<C<3b | C. | 2a+b<C<a+2b | D. | 2(a+b)<C<a+3b |
 如图,D是△ABC的BA边延长线上的一点,AE是∠DAC的平分线,∠B=∠C,试说明:AE∥BC.
如图,D是△ABC的BA边延长线上的一点,AE是∠DAC的平分线,∠B=∠C,试说明:AE∥BC. 如图,Rt△ABC中,∠C=90°,用直尺和圆规在边BC上找一点D,使D到AB的距离等于CD.(保留作图痕迹,不写作法)
如图,Rt△ABC中,∠C=90°,用直尺和圆规在边BC上找一点D,使D到AB的距离等于CD.(保留作图痕迹,不写作法)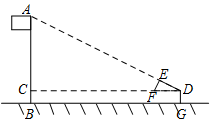 如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行并使直角边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,且测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=25米,求旗杆AB的高度.
如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行并使直角边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,且测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=25米,求旗杆AB的高度.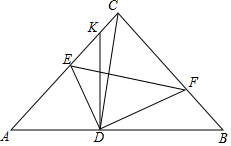 如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.
如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.