题目内容
2.先化简,再求值(1)5a(a-b)-(a+b)(a-b)-(2a+b)2,其中a=$\frac{1}{3}$,b=-2.
(2)(x-$\frac{1-3x}{x-3}$)•$\frac{6-2x}{{x}^{2}+2x+1}$,其中x=-$\frac{1}{2}$.
分析 (1)首先化简5a(a-b)-(a+b)(a-b)-(2a+b)2,然后把a=$\frac{1}{3}$,b=-2代入化简后的算式,求出算式的值是多少即可.
(2)首先化简(x-$\frac{1-3x}{x-3}$)•$\frac{6-2x}{{x}^{2}+2x+1}$,然后把x=-$\frac{1}{2}$代入化简后的算式,求出算式的值是多少即可.
解答 解:(1)5a(a-b)-(a+b)(a-b)-(2a+b)2
=5a2-5ab-a2+b2-4a2-4ab-b2
=-9ab
当a=$\frac{1}{3}$,b=-2时,
原式=-9×$\frac{1}{3}$×(-2)=6
(2)(x-$\frac{1-3x}{x-3}$)•$\frac{6-2x}{{x}^{2}+2x+1}$
=$\frac{{x}^{2}-1}{x-3}$•$\frac{6-2x}{{x}^{2}+2x+1}$
=$\frac{2(1-x)}{1+x}$
当x=-$\frac{1}{2}$时,
原式=$\frac{2[1-(-\frac{1}{2})]}{1+(-\frac{1}{2})}$=6.
点评 此题主要考查了整式的混合运算-化简求值,以及分式的化简求值问题,要熟练掌握,注意先把分式化简后,再把分式中未知数对应的值代入求出分式的值.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
13.已知三角形两边长分别是a,b(b>a),则三角形的周长C应满足( )
| A. | 2b<C<2(a+b) | B. | a+b<C<3b | C. | 2a+b<C<a+2b | D. | 2(a+b)<C<a+3b |
17.为鼓励居民节约用电,某省试行阶段电价收费制,具体执行方案如表:
(1)若一户居民七月份用电420度,则需缴电费多少元?
(2)若一户居民某月用电x度(x大于200小于400),则需缴电费多少元?(用含x的代数式表示)
(3)某户居民五、六月份共用电500度,缴电费262元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度,问该户居民五、六月份各用电多少度?
| 档次 | 每户每月用电数(度) | 执行电价(元/度) |
| 第一档 | 小于200部分 | 0.5 |
| 第二档 | 200小于等于400部分 | 0.6 |
| 第三档 | 大于400部分 | 0.8 |
(2)若一户居民某月用电x度(x大于200小于400),则需缴电费多少元?(用含x的代数式表示)
(3)某户居民五、六月份共用电500度,缴电费262元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度,问该户居民五、六月份各用电多少度?
 如图,在正方形ABCD中,E、F分别是AB,BC上一点,EG⊥AF于H,交CD于点G,求证:BE+BF=CG.
如图,在正方形ABCD中,E、F分别是AB,BC上一点,EG⊥AF于H,交CD于点G,求证:BE+BF=CG.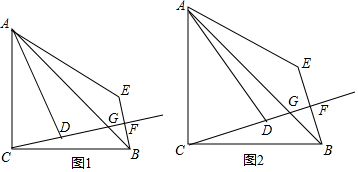
 如图,在长为70米,宽为40米的长方形空地中,张老板想在上面修建焯天茶餐厅和子欣西餐厅,两所餐厅的四周铺上等宽的小路隔开,如果小路的面积占总面积的八分之一,求小路的宽度是多少?
如图,在长为70米,宽为40米的长方形空地中,张老板想在上面修建焯天茶餐厅和子欣西餐厅,两所餐厅的四周铺上等宽的小路隔开,如果小路的面积占总面积的八分之一,求小路的宽度是多少?