题目内容
17.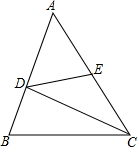 如图,在△ABC中,E点为AC的中点,其中BD=1,DC=3,BC=$\sqrt{10}$,AD=$\sqrt{7}$,求DE的长.
如图,在△ABC中,E点为AC的中点,其中BD=1,DC=3,BC=$\sqrt{10}$,AD=$\sqrt{7}$,求DE的长.
分析 首先根据勾股定理的逆定理判定△BCD是直角三角形且∠BDC=90°,再利用勾股定理可求出AC的长,进而可求出DE的长.
解答 解:∵BD=1,DC=3,BC=$\sqrt{10}$,
又∵12+32=($\sqrt{10}$)2,
∴BD2+CD2=BC2,
∴△BCD是直角三角形且∠BDC=90°,
∴∠ADC=90°,
∴AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=4,
又∵E点为AC的中点
∴DE=$\frac{AC}{2}$=2.
点评 本题考查了勾股定理以及其逆定理的运用,首先要证明三角形BCD是直角三角形且∠BDC=90°是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
8.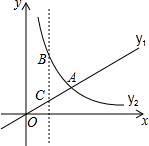 已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )
已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )
 已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )
已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )| A. | 两函数图象的交点坐标为($\sqrt{3}$,1)或(-$\sqrt{3}$,-1) | |
| B. | 当x>$\sqrt{3}$时,y2>y1 | |
| C. | 当x=1时,BC=2$\sqrt{3}$ | |
| D. | 当x=1时,△ABC的面积为1-$\frac{\sqrt{3}}{3}$ |
2.无理数$\sqrt{5}$的整数部分是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
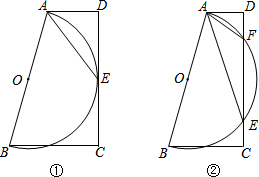 在梯形ABCD中,AD∥BC,∠D=90°,以AB为直径作⊙O.
在梯形ABCD中,AD∥BC,∠D=90°,以AB为直径作⊙O.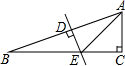 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交AB于D,交BC于E,若CE=1,∠AEC=45°,则BE的长是$\sqrt{2}$.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交AB于D,交BC于E,若CE=1,∠AEC=45°,则BE的长是$\sqrt{2}$.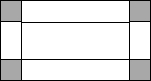 如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为11cm.
如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为11cm.