题目内容
18.若x<0,则$\frac{\sqrt{{x}^{2}}}{x}$的结果是-1.分析 利用x的取值范围,进而化简求出即可.
解答 解:∵x<0,
∴$\frac{\sqrt{{x}^{2}}}{x}$=$\frac{-x}{x}$=-1.
故答案为:-1.
点评 此题主要考查了二次根式的化简,正确利用二次根式的性质进行化简是解题关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
8.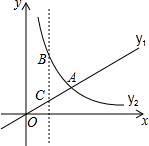 已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )
已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )
 已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )
已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )| A. | 两函数图象的交点坐标为($\sqrt{3}$,1)或(-$\sqrt{3}$,-1) | |
| B. | 当x>$\sqrt{3}$时,y2>y1 | |
| C. | 当x=1时,BC=2$\sqrt{3}$ | |
| D. | 当x=1时,△ABC的面积为1-$\frac{\sqrt{3}}{3}$ |
3.下列标识中,既是轴对称图形,又是中心对称图形的是( )
| A. | 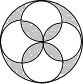 | B. | 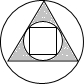 | C. |  | D. |  |
10. 某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完全资料,已知点A的坐标为(2,10),请你结合表格和图象:
某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完全资料,已知点A的坐标为(2,10),请你结合表格和图象:
(1)指出付款金额和购买量哪个变量是函数的自变量x,并写出表中a、b的值;
(2)求出当x>2时,y关于x的函数解析式;
(3)甲衣户将8.8元钱全部用了购买该玉米种子,乙农户购买了4165克该玉米种子,分别计算他们的购买量和付款金额.
 某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完全资料,已知点A的坐标为(2,10),请你结合表格和图象:
某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完全资料,已知点A的坐标为(2,10),请你结合表格和图象:| 付款金额(元) | a | 7.5 | 10 | 12 | b |
| 购买量(千克) | 1 | 1.5 | 2 | 2.5 | 3 |
(2)求出当x>2时,y关于x的函数解析式;
(3)甲衣户将8.8元钱全部用了购买该玉米种子,乙农户购买了4165克该玉米种子,分别计算他们的购买量和付款金额.
8.若一个点的横坐标与纵坐标互为相反数,则此点一定在( )
| A. | 原点 | B. | 横轴上 | ||
| C. | 第二、四象限角平分线上 | D. | 第一、三象限角平分线上 |
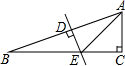 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交AB于D,交BC于E,若CE=1,∠AEC=45°,则BE的长是$\sqrt{2}$.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交AB于D,交BC于E,若CE=1,∠AEC=45°,则BE的长是$\sqrt{2}$.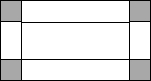 如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为11cm.
如图,一块矩形铁皮的长是宽的2倍,将这个铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,若盒子的容积是240cm3,则原铁皮的宽为11cm.