题目内容
18. 如图所示,两个完全一样的正方形ABOC和正方形DEMF,正方形DEMF的顶点E与正方形ABOC的中心重合,将正方形DEMF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=5.
如图所示,两个完全一样的正方形ABOC和正方形DEMF,正方形DEMF的顶点E与正方形ABOC的中心重合,将正方形DEMF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=5.
分析 首先得出△BEP∽△CQE,进而求出BE的长,再得出△BEG∽△EPG,即可得出$\frac{BE}{EP}$=$\frac{BG}{EG}$=$\frac{EG}{PG}$,求出PG的长即可.
解答 解:∵∠QEC=180°-∠DEF-∠BEP=135°-∠BEP,
∠BPE=180°-∠PBE-∠BEP=135°-∠BEP,
∴∠QEC=∠BPE,
又∵∠PBE=∠EQC=45°,
∴△BEP∽△CQE,
∴$\frac{BE}{QC}$=$\frac{BP}{EC}$,
设EC=x,则BE=x,AC=$\sqrt{2}$x,
故$\frac{x}{12+\sqrt{2}x}$=$\frac{3}{x}$,
解得:x1=6$\sqrt{2}$,x2=-3$\sqrt{2}$(舍去),
∴AB=AC=6$\sqrt{2}$×$\sqrt{2}$=12,则AP=9,
过点P作PN⊥BE于点N,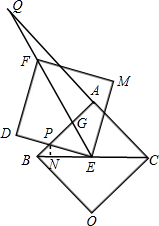
∵BP=3,∠B=45°,
∴BN=PN=$\frac{3\sqrt{2}}{2}$,
故NE=$\frac{9\sqrt{2}}{2}$,
则PE=3$\sqrt{5}$,
∵∠EBG=∠PEG,∠BGE=∠EGP,
∴△BEG∽△EPG,
∴$\frac{BE}{EP}$=$\frac{BG}{EG}$=$\frac{EG}{PG}$,
设PG=y,
∴$\frac{6\sqrt{2}}{3\sqrt{5}}$=$\frac{3+y}{EG}$=$\frac{EG}{y}$,
解得:y=5.
故答案为:5.
点评 此题主要考查了旋转的性质以及正方形的性质和勾股定理以及相似三角形的判定与性质等知识,得出PE的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.如果圆O是△ABC的外接圆,AC=BC,那么下列四个选项中,直线l必过圆心O的是( )
| A. | l⊥AC | B. | l平分AB | C. | l平分∠C | D. | l平分$\widehat{AB}$ |
3.要使(y2-ky+2y)(-y)的展开式中不含y2项,则k的值为( )
| A. | -2 | B. | 0 | C. | 2 | D. | 3 |
10.若二次函数y=-x2-3x+2的自变量x分别取x1、x2、x3,且x1、x2、x3,且0<x1<x2<x3,则对应的函数值y1、y2、y3的大小关系正确的是( )
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y1<y3<y2 | D. | y2<y3<y1 |
7.如图,若AB∥CD,则α、β,γ之间的关系为( )


| A. | α+β+γ=360° | B. | α+β-γ=180° | C. | α+β+γ=180° | D. | α-β+γ=180° |
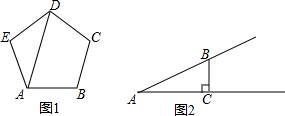
 如图所示,把一张长方形的纸条ABCD沿对角线BD将△BCD折成△BDF,DF交AB于E,若已知AE=2cm,∠BDC=30°,求纸条的长和宽各是6,2$\sqrt{3}$.
如图所示,把一张长方形的纸条ABCD沿对角线BD将△BCD折成△BDF,DF交AB于E,若已知AE=2cm,∠BDC=30°,求纸条的长和宽各是6,2$\sqrt{3}$.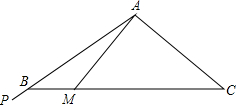 在等腰△ABC中AB=AC,∠BAC=120°,在边AB的延长线上有一点P,射线AP从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.当AP旋转1秒时,此时光线AP交BC于点M,BM的长为(20$\sqrt{3}$-20)cm,光线AP从AB处旋转开始计时,若要转2018秒,射线AP与BC边的交点与点B之间的距离是(20$\sqrt{3}$-10)cm.
在等腰△ABC中AB=AC,∠BAC=120°,在边AB的延长线上有一点P,射线AP从AB开始,绕点A逆时针匀速旋转,每秒钟旋转15°,到达AC后立即以相同旋转速度返回AB,到达后立即重复上述旋转过程.当AP旋转1秒时,此时光线AP交BC于点M,BM的长为(20$\sqrt{3}$-20)cm,光线AP从AB处旋转开始计时,若要转2018秒,射线AP与BC边的交点与点B之间的距离是(20$\sqrt{3}$-10)cm.