题目内容
6. 如图所示,把一张长方形的纸条ABCD沿对角线BD将△BCD折成△BDF,DF交AB于E,若已知AE=2cm,∠BDC=30°,求纸条的长和宽各是6,2$\sqrt{3}$.
如图所示,把一张长方形的纸条ABCD沿对角线BD将△BCD折成△BDF,DF交AB于E,若已知AE=2cm,∠BDC=30°,求纸条的长和宽各是6,2$\sqrt{3}$.
分析 由轴对称的性质可以求出∠BDC=∠BDF,进而可以求出∠ADE的值,就可以求出AD及AE的长,再由等腰三角形的性质即可得出BE的长,进而可得出结论.
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴AD=BC,AB=CD,∠A=∠ABC=∠C=∠ADC=90°,AD∥BC,
∴∠EBD=∠BDC.
∵△BDC与△BDF成轴对称,
∴∠BDC=∠BDF.
∵∠BDC=30°,
∴∠BDF=30°,∠EDB=30°,
∴∠ADE=30°,∠EDB=∠EBD,
∴BE=DE.
∵∠ADE=30°,AE=2,
∴DE=2AE=4.
∴BE=4,
∴AB=AE+BE=2+4=6,AD=$\frac{AE}{tan30°}$=$\frac{2}{\frac{\sqrt{3}}{3}}$=2$\sqrt{3}$.
故答案为:6,2$\sqrt{3}$.
点评 本题考查的是翻折变换,涉及到轴对称性质的运用,直角三角形的性质的运用,平行线的性质的运用,等腰三角形的判定及性质的运用,解答时灵活运用轴对称的性质求解是关键.

练习册系列答案
相关题目
6.某种计算机完成一次基本运算所用的时间约为0.0000000051s,把0.0000000051用科学记数法可表示为( )
| A. | 0.51×10-8 | B. | 1.5×10-8 | C. | 1.5×10-9 | D. | 0.15×10-9 |
 如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)正方形的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A2016的坐标为(504,-504).
如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)正方形的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A2016的坐标为(504,-504).




 观察下列各个等式:
观察下列各个等式: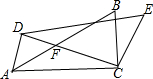 如图,△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕点C按顺时针方向旋转,旋转角为α(0°<α<90°),得到△DEC,设CD交AB于点F,连接AD,当α=40°时,AD=AF.
如图,△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕点C按顺时针方向旋转,旋转角为α(0°<α<90°),得到△DEC,设CD交AB于点F,连接AD,当α=40°时,AD=AF. 如图所示,两个完全一样的正方形ABOC和正方形DEMF,正方形DEMF的顶点E与正方形ABOC的中心重合,将正方形DEMF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=5.
如图所示,两个完全一样的正方形ABOC和正方形DEMF,正方形DEMF的顶点E与正方形ABOC的中心重合,将正方形DEMF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=5. 如图,半径为2cm的圆O与地面相切于点B,圆周上一点A距地面高为(2+$\sqrt{3}$)cm,圆O沿地面BC方向滚动,当点A第一次接触地面时,圆O在地面上滚动的距离为$\frac{5π}{3}$cm.
如图,半径为2cm的圆O与地面相切于点B,圆周上一点A距地面高为(2+$\sqrt{3}$)cm,圆O沿地面BC方向滚动,当点A第一次接触地面时,圆O在地面上滚动的距离为$\frac{5π}{3}$cm.