题目内容
1. 如图,在每个小正方形的边长均为1的方格纸中有线段AC和EF,点A、C、E、F均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中有线段AC和EF,点A、C、E、F均在小正方形的顶点上.(1)在方格纸中画出一个以AC为对角线的菱形ABCD,点D在直线AC的下方,且点B、D都在小正方形的顶点上;
(2)在方格纸中画出以EF为底边,面积为6的等腰三角形EFG,且点G在小正方形的顶点上;
(3)在(1)、(2)的条件下,连接DG,请直接写出线段DG的长.
分析 (1)画出AC的垂直平分线即可解决问题;
(2)画出线段EF的垂直平分线,再根据高的值即可确定点G的位置;
(3)利用勾股定理即可解决问题;
解答 解:(1)菱形ABCD如图所示.
(2)△EFG如图所示.(EF=2$\sqrt{2}$,三角形的高=3$\sqrt{2}$)
(3)DG=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
点评 本题考查勾股定理、菱形的判定等知识,解题的关键是灵活应用所学知识解决问题,利用数形结合的思想解决问题,属于中考常考题型.

练习册系列答案
相关题目
11.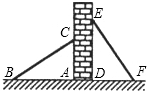 如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角∠ABC=35°,则右边的滑梯与地面的夹角∠DFE=( )
如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角∠ABC=35°,则右边的滑梯与地面的夹角∠DFE=( )
 如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角∠ABC=35°,则右边的滑梯与地面的夹角∠DFE=( )
如图,有两个长度相同的滑梯靠在一面墙上,已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,且左边的滑梯与地面的夹角∠ABC=35°,则右边的滑梯与地面的夹角∠DFE=( )| A. | 60° | B. | 55° | C. | 65° | D. | 35° |
9.已知函数y=2x+b的图象过点(2,3),当 x=3时,y的值是( )
| A. | 4 | B. | 5 | C. | 8 | D. | 7 |
16.若一个三角形的三边长分别为5、7、x-2,则x的取值范围是( )
| A. | 0<x<14 | B. | 4<x<14 | C. | 0<x<10 | D. | 2<x<10 |
6. 如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于( )
如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于( )
 如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于( )
如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于( )| A. | 100° | B. | 112.5° | C. | 120° | D. | 135° |
13.若a,b为两质数且相差2,则ab+1之值可能为下列何者( )
| A. | 392 | B. | 402 | C. | 412 | D. | 422 |
 在如图所示的直角坐标系中,解答下列问题:
在如图所示的直角坐标系中,解答下列问题: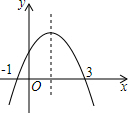 如图是二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0,其中正确的是②③④(填序号)
如图是二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0,其中正确的是②③④(填序号)