题目内容

6．如图，四边形ABCD内接于⊙O，AB经过圆心，∠B=3∠BAC，则∠ADC等于（　　）
A．100°B．112.5°C．120°D．135°

分析 由AB是⊙O的直径，得到∠CAB+∠B=90°，根据∠B=3∠BAC，求得∠B=67.5，根据圆内接四边形的性质即可得到结论．

解答 解：∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠CAB+∠B=90°，
∵∠B=3∠BAC，
∴∠B=67.5，
∵四边形ABCD内接于⊙O，
∴∠ADC=180°-∠B=112.5°，
故选B．

点评 此题主要考查了圆周角定理以及圆内接四边形的性质，得出∠B的度数是解题关键．

练习册系列答案
相关题目
16．等腰三角形的两边的长分别为2cm和7cm，则三角形的周长是（　　）
A．11B．16C．11或16D．无法计算
17．解不等式（组）：（请把解集在数轴上表示出来）
（1）2（x+1）-1≥3x+2
（2）$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3（x-1）＜8-x}\end{array}\right.$．
14．因式分解：
（1）4a4-64；
（2）81x4-72x2y2+16y4．
1．如图，在每个小正方形的边长均为1的方格纸中有线段AC和EF，点A、C、E、F均在小正方形的顶点上．
（1）在方格纸中画出一个以AC为对角线的菱形ABCD，点D在直线AC的下方，且点B、D都在小正方形的顶点上；
（2）在方格纸中画出以EF为底边，面积为6的等腰三角形EFG，且点G在小正方形的顶点上；
（3）在（1）、（2）的条件下，连接DG，请直接写出线段DG的长．
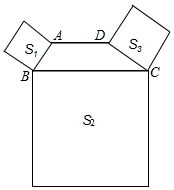11．如图，四边形ABCD中，AD∥BC，∠ABC+∠DCB=90°，且BC=2AD，以AB、BC、DC为边向外作正方形，其面积分别为S1、S2、S3，若S1=3，S3=9，则S2的值为（　　）
A．12B．18C．24D．48
18．用代入法解方程
$\left\{\begin{array}{l}{4x=5+y}\\{\frac{x}{2}+\frac{y}{3}=2}\end{array}\right.$．
15．如图，已知点O（0，0），A（2，1），抛物线l：y=-（x-h）2+1（h为常数）与y轴的交点为B．
（1）若l经过点A，求它的解析式，并写出此时l的对称轴及顶点坐标；
（2）设点B的纵坐标yB，求yB的最大值，此时l上有两点（x1，y1），（x2，y2），其中x1＞x2≥0，比较y1与y2的大小．
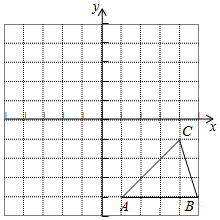16．已知，方格纸中的每个小正方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，-1）．
（1）把△ABC向上平移5个单位后得到对应的△A1B1C1，画出△A1B1C1，并写出C1的坐标；
（2）以y轴为对称轴，画出与△A1B1C1对称的△A2B2C2，并写出A2、B2、C2的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网