题目内容
5.教室里的饮水机接通电源就进入自动程序,开机加热时水温上升,加热到100℃停止加热,水温开始下降,水温降至30℃,饮水机自动开始加热,重复上述程序.值日生小明7点钟到校后接通饮水机电源,在水温下降的过程中进行了水温检测,记录如下表:| 时间x | 7:00 | 7:02 | 7:05 | 7:07 | 7:10 | 7:14 | 7:20 |
| 水温y | 30℃ | 50℃ | 80℃ | 100℃ | 70℃ | 50℃ | 35℃ |
(2)借助(1)所画的图象,判断从7:00开始加温到水温第一次降到30℃为止,水温y和时间x之间存在怎样的函数关系?试求出函数关系并写出自变量x取值范围;
(3)上午第一节下课时间为8:25,同学们能不能喝到不超过50℃的水?请通过计算说明.
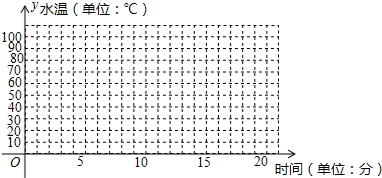
分析 (1)根据表格中数据,先描点,再用平滑的曲线按照自变量从小到大的顺序依次连接各点可得图象;
(2)由函数图象可设函数解析式,再由图中坐标代入解析式,即可求得y与x的关系式;
(3)求出饮水机完成一个循环周期所需要的时间,再计算求出每一个循环周期内,水温超过50℃的时间段,最后根据时间确定答案.
解答 解:(1)图象如下:
(2)由图象可知,在加热过程中y是x的一次函数,故设y1=kx+b,
将(0,30),(2,50)代入,得:$\left\{\begin{array}{l}{b=30}\\{2k+b=50}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=10}\\{b=30}\end{array}\right.$,
故y1=10x+30,(0≤x≤7);
在降温过程中y是x的反比例函数,可设y2=$\frac{m}{x}$,
将(10,70)代入,得m=700,
故y2=$\frac{700}{x}$,
当y=30时,x=$\frac{70}{3}$,故降温过程中7≤x≤$\frac{70}{3}$;
(3)将y=50分别代入以上两个解析式,得x1=2,x2=14,
将y=30代入y2=$\frac{700}{x}$,得x=$\frac{70}{3}$,即饮水机一个循环周期为$\frac{70}{3}$分钟,
每个循环周期内,当0≤x≤2及14≤x≤$\frac{70}{3}$时,水温不超过50℃,
而7:00至8:25共85分钟,85-3×$\frac{70}{3}$=15,
∵14≤15≤$\frac{70}{3}$,
∴8:25时同学们能喝到不超过50℃的水.
点评 本题主要考查了一次函数及反比例函数的应用题,还有时间的讨论问题.关键是要正确理解题意,计算出饮水机的一个循环周期所用时间.

 如图,在△ABC中,∠A=36°,AB=AC,BD⊥AC于点D,则∠DBC=( )
如图,在△ABC中,∠A=36°,AB=AC,BD⊥AC于点D,则∠DBC=( )| A. | 8° | B. | 18° | C. | 28° | D. | 44° |
 如图,BC是⊙O的直径,点B、C、E、D都在⊙O上,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=( )
如图,BC是⊙O的直径,点B、C、E、D都在⊙O上,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=( )| A. | sinA | B. | sin2A | C. | cosA | D. | cos2A |
| A. | -(-2) | B. | -|-2| | C. | -22 | D. | (-2)2 |
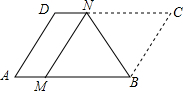 如图,将平行四边形纸片ABCD折叠,使顶点C恰好落在AB边上的点M处,折痕为BN,则关于结论:①MN∥AD;②MNCB是菱形.说法正确的是( )
如图,将平行四边形纸片ABCD折叠,使顶点C恰好落在AB边上的点M处,折痕为BN,则关于结论:①MN∥AD;②MNCB是菱形.说法正确的是( )| A. | ①②都错 | B. | ①对②错 | C. | ①错②对 | D. | ①②都对 |
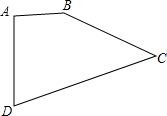 如图,已知四边形ABCD中,AB=2cm,BC=4cm,CD=5cm,AD=$\sqrt{5}$cm,∠A=90°,求四边形ABCD的面积.
如图,已知四边形ABCD中,AB=2cm,BC=4cm,CD=5cm,AD=$\sqrt{5}$cm,∠A=90°,求四边形ABCD的面积. 一艘轮船与一艘快船沿相同方向行驶,轮船与快艇行驶过程中路程随时间变化的图象如图所示,请解答下列问题:
一艘轮船与一艘快船沿相同方向行驶,轮船与快艇行驶过程中路程随时间变化的图象如图所示,请解答下列问题: