题目内容
13.有两把不同的锁和三把钥匙,其中两把钥匙分别能打开这两把锁,第三把钥匙不能打开这两把锁.现在随机取出一把钥匙去开任意一把锁.(1)请用列表或画树状图的方法表示出上述试验所有可能结果;
(2)求一次打开锁的概率.
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由(1)中的树状图,可求得一次打开锁的情况,再利用概率公式求解即可求得答案.
解答 解:(1)设两把不同的锁为A、B,能把两锁打开的钥匙分别为a、b,第三把钥匙为c,根据题意,可以画出如下树形图:
由上图可知,上述试验所有可能结果分别为Aa,Ab,Ac,Ba,Bb,Bc.
(2)由(1)可知,任意取出一把钥匙去开任意一把锁共有6种可能的结果,一次打开锁的结果有2种,且所有结果的可能性相等.
∴P(一次打开锁)=$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比

练习册系列答案
相关题目
1.下列各点中,在函数y=-$\frac{4}{x}$图象上的是( )
| A. | (-1,4) | B. | (2,2) | C. | (-1,-4) | D. | (4,1) |
5.教室里的饮水机接通电源就进入自动程序,开机加热时水温上升,加热到100℃停止加热,水温开始下降,水温降至30℃,饮水机自动开始加热,重复上述程序.值日生小明7点钟到校后接通饮水机电源,在水温下降的过程中进行了水温检测,记录如下表:
(1)在图中的平面直角坐标系,画出水温y关于饮水机接通电源时间x的函数图象;
(2)借助(1)所画的图象,判断从7:00开始加温到水温第一次降到30℃为止,水温y和时间x之间存在怎样的函数关系?试求出函数关系并写出自变量x取值范围;
(3)上午第一节下课时间为8:25,同学们能不能喝到不超过50℃的水?请通过计算说明.
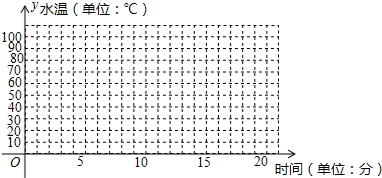
| 时间x | 7:00 | 7:02 | 7:05 | 7:07 | 7:10 | 7:14 | 7:20 |
| 水温y | 30℃ | 50℃ | 80℃ | 100℃ | 70℃ | 50℃ | 35℃ |
(2)借助(1)所画的图象,判断从7:00开始加温到水温第一次降到30℃为止,水温y和时间x之间存在怎样的函数关系?试求出函数关系并写出自变量x取值范围;
(3)上午第一节下课时间为8:25,同学们能不能喝到不超过50℃的水?请通过计算说明.

 如图,AD,AE分别是△ABC的高和中线,已知AD=5,CE=4,则△ABC的面积为20.
如图,AD,AE分别是△ABC的高和中线,已知AD=5,CE=4,则△ABC的面积为20.