题目内容

15．如图，在△ABC中，∠A=36°，AB=AC，BD⊥AC于点D，则∠DBC=（　　）
A．8°B．18°C．28°D．44°

分析 根据已知可求得两底角的度数，再根据三角形内角和定理不难求得∠DBC的度数．

解答 解：∵AB=AC，∠A=36°，
∴∠ABC=∠ACB=72°．
∵BD⊥AC于点D，
∴∠CBD=90°-72°=18°．
故选B．

点评 本题主要考查等腰三角形的性质，解答本题的关键是会综合运用等腰三角形的性质和三角形的内角和定理进行答题，此题难度一般．

练习册系列答案
相关题目
5．如图，在Rt△ABC中，∠C=90°，AC=BC=4，点P是AB边中点，∠MPN=90°，∠MPN绕点P旋转．
（1）如图1，在旋转过程中，PM、PN分别与边AC、CB相交于点D、E，求证：PD=PE；
（2）如图2，在旋转过程中，PM，PN分别与边AC、CB的延长线相交于点D、E．PD=PE还成立吗？请说明理由；
（3）在（1）中，若△PAD是等腰三角形，请直接写出使△PAD是等腰是三角形时的CE长．
6．在平面直角坐标系中，⊙P的圆心坐标为（4，8），半径为5，那么x轴与⊙P的位置关系是（　　）
A．相交B．相离C．相切D．以上都不是
3．已知A、B、C三点在一条直线上，且线段AB=15cm，BC=5cm，则线段AC=20cm或10cm．
10．如图1，在△ABC中，∠C=90°，点D在BC上，DE⊥AB于点E，点M是AD的中点，连接CM、EM．
（1）问题发现：
①线段CM、EM的数量关系是CM=ME；
②∠CME、∠CAB的数量关系是∠CME=2∠CAB．
（2）拓展探究：
将△BED绕着点B旋转到图2的位置时，小明猜想（1）中的结论①②仍然成立，并尝试取AB的中点G和BD的中点F．作了△CGM和△MFE，请你证明小明的猜想．
（3）问题解决：
已知∠B=30°，BD=AC=4，当△BED旋转至A、D、E三点共线时，直接写出线段CM的长．
20．分解因式：3xy2+6xy+3x=2x（y+1）2．
7．如图，点P、Q是∠AOB内部的两个定点，点M是∠AOB内部的一点，且点M到OA、OB的距离相等，点M到点P、点Q的距离相等，请利用直尺和圆规作出点M．（不写作法，保留作图痕迹）
4．如图，AD，AE分别是△ABC的高和中线，已知AD=5，CE=4，则△ABC的面积为20．
5．教室里的饮水机接通电源就进入自动程序，开机加热时水温上升，加热到100℃停止加热，水温开始下降，水温降至30℃，饮水机自动开始加热，重复上述程序．值日生小明7点钟到校后接通饮水机电源，在水温下降的过程中进行了水温检测，记录如下表：
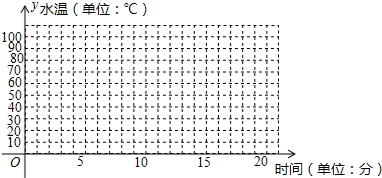
时间x7：007：027：057：077：107：147：20
水温y30℃50℃80℃100℃70℃50℃35℃
（1）在图中的平面直角坐标系，画出水温y关于饮水机接通电源时间x的函数图象；
（2）借助（1）所画的图象，判断从7：00开始加温到水温第一次降到30℃为止，水温y和时间x之间存在怎样的函数关系？试求出函数关系并写出自变量x取值范围；
（3）上午第一节下课时间为8：25，同学们能不能喝到不超过50℃的水？请通过计算说明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网