题目内容
20.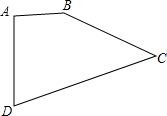 如图,已知四边形ABCD中,AB=2cm,BC=4cm,CD=5cm,AD=$\sqrt{5}$cm,∠A=90°,求四边形ABCD的面积.
如图,已知四边形ABCD中,AB=2cm,BC=4cm,CD=5cm,AD=$\sqrt{5}$cm,∠A=90°,求四边形ABCD的面积.
分析 连接BD,根据勾股定理求出BD的长,根据勾股定理的逆定理判断△BDC是直角三角形,根据直角三角形的面积公式计算即可.
解答 解: 连接BD,
连接BD,
∵∠A=90°,AB=2cm,AD=$\sqrt{5}$cm,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=3cm,△ABD的面积为:$\frac{1}{2}$×AB×AD=$\sqrt{5}$cm2,
∵BD2+BC2=25,CD2=25,
∴BD2+BC2=CD2,
∴∠BDC=90°,
∴△BDC的面积为:$\frac{1}{2}$×BD×BC=6cm2,
∴四边形ABCD的面积=△ABD的面积+△BDC的面积=(6+$\sqrt{5}$)cm2.
点评 本题考查的是勾股定理和勾股定理的逆定理的应用,在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知点(-1,y1),(2,y2)都在直线y=$\frac{1}{2}$x+b上,则y1,y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
5.教室里的饮水机接通电源就进入自动程序,开机加热时水温上升,加热到100℃停止加热,水温开始下降,水温降至30℃,饮水机自动开始加热,重复上述程序.值日生小明7点钟到校后接通饮水机电源,在水温下降的过程中进行了水温检测,记录如下表:
(1)在图中的平面直角坐标系,画出水温y关于饮水机接通电源时间x的函数图象;
(2)借助(1)所画的图象,判断从7:00开始加温到水温第一次降到30℃为止,水温y和时间x之间存在怎样的函数关系?试求出函数关系并写出自变量x取值范围;
(3)上午第一节下课时间为8:25,同学们能不能喝到不超过50℃的水?请通过计算说明.
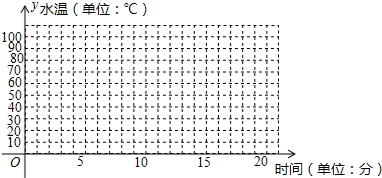
| 时间x | 7:00 | 7:02 | 7:05 | 7:07 | 7:10 | 7:14 | 7:20 |
| 水温y | 30℃ | 50℃ | 80℃ | 100℃ | 70℃ | 50℃ | 35℃ |
(2)借助(1)所画的图象,判断从7:00开始加温到水温第一次降到30℃为止,水温y和时间x之间存在怎样的函数关系?试求出函数关系并写出自变量x取值范围;
(3)上午第一节下课时间为8:25,同学们能不能喝到不超过50℃的水?请通过计算说明.

9.下列四个数中,负数是( )
| A. | |-2| | B. | -22 | C. | -(-2) | D. | $\sqrt{(-2)^{2}}$ |
 阅读下列材料:小华遇到这样一个问题:
阅读下列材料:小华遇到这样一个问题: 某水果大卖场每日批量进货销售某种水果,假设日销售量与日进货量相等.设该水果进货量为x千克,每千克进货成本为y元,每千克售价为s元,y与x的关系如图,s与x满足关系式:s=-$\frac{1}{15}$x+12.
某水果大卖场每日批量进货销售某种水果,假设日销售量与日进货量相等.设该水果进货量为x千克,每千克进货成本为y元,每千克售价为s元,y与x的关系如图,s与x满足关系式:s=-$\frac{1}{15}$x+12.