题目内容
16.如果ab>0,a+b<0,那么下面各式:①$\sqrt{\frac{a}{b}}$=$\frac{\sqrt{a}}{\sqrt{b}}$,②$\sqrt{\frac{a}{b}}$$•\sqrt{\frac{b}{a}}$=1,③$\sqrt{ab}$÷$\sqrt{\frac{a}{b}}$=-b,其中正确的是②③(填序号)分析 由ab>0,a+b<0,可得出a<0,b<0,从而排除了①,再根据二次根式乘除法运算法则可得知②③正确.
解答 解:∵ab>0,a+b<0,
∴a<0,b<0.
①根号下必须非负,错误;
②$\sqrt{\frac{a}{b}}$$•\sqrt{\frac{b}{a}}$=$\sqrt{\frac{a}{b}×\frac{b}{a}}$=1,正确;
③$\sqrt{ab}$÷$\sqrt{\frac{a}{b}}$=$\sqrt{ab÷\frac{a}{b}}$=$\sqrt{{b}^{2}}$=-b,正确.
故答案为:②③.
点评 本题考查了二次根式的乘除法,解题的关键是:能熟练的运用二次根式乘除法的运算法则,并知道根号下必须非负.

练习册系列答案
相关题目
6.在平面直角坐标系中,⊙P的圆心坐标为(4,8),半径为5,那么x轴与⊙P的位置关系是( )
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 以上都不是 |
1.下列各点中,在函数y=-$\frac{4}{x}$图象上的是( )
| A. | (-1,4) | B. | (2,2) | C. | (-1,-4) | D. | (4,1) |
5.教室里的饮水机接通电源就进入自动程序,开机加热时水温上升,加热到100℃停止加热,水温开始下降,水温降至30℃,饮水机自动开始加热,重复上述程序.值日生小明7点钟到校后接通饮水机电源,在水温下降的过程中进行了水温检测,记录如下表:
(1)在图中的平面直角坐标系,画出水温y关于饮水机接通电源时间x的函数图象;
(2)借助(1)所画的图象,判断从7:00开始加温到水温第一次降到30℃为止,水温y和时间x之间存在怎样的函数关系?试求出函数关系并写出自变量x取值范围;
(3)上午第一节下课时间为8:25,同学们能不能喝到不超过50℃的水?请通过计算说明.
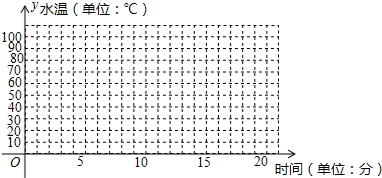
| 时间x | 7:00 | 7:02 | 7:05 | 7:07 | 7:10 | 7:14 | 7:20 |
| 水温y | 30℃ | 50℃ | 80℃ | 100℃ | 70℃ | 50℃ | 35℃ |
(2)借助(1)所画的图象,判断从7:00开始加温到水温第一次降到30℃为止,水温y和时间x之间存在怎样的函数关系?试求出函数关系并写出自变量x取值范围;
(3)上午第一节下课时间为8:25,同学们能不能喝到不超过50℃的水?请通过计算说明.

 如图,点P、Q是∠AOB内部的两个定点,点M是∠AOB内部的一点,且点M到OA、OB的距离相等,点M到点P、点Q的距离相等,请利用直尺和圆规作出点M.(不写作法,保留作图痕迹)
如图,点P、Q是∠AOB内部的两个定点,点M是∠AOB内部的一点,且点M到OA、OB的距离相等,点M到点P、点Q的距离相等,请利用直尺和圆规作出点M.(不写作法,保留作图痕迹) 如图,AD,AE分别是△ABC的高和中线,已知AD=5,CE=4,则△ABC的面积为20.
如图,AD,AE分别是△ABC的高和中线,已知AD=5,CE=4,则△ABC的面积为20.