题目内容
14. 一艘轮船与一艘快船沿相同方向行驶,轮船与快艇行驶过程中路程随时间变化的图象如图所示,请解答下列问题:
一艘轮船与一艘快船沿相同方向行驶,轮船与快艇行驶过程中路程随时间变化的图象如图所示,请解答下列问题:(1)分别写出表示轮船和快艇行驶过程中路程y(千米)和时间x(小时)的函数关系式(不需写自变量的取值范围);
(2)轮船和快艇在途中行驶的速度分别是多少?
(3)快艇出发多长时间追上轮船?
分析 根据图象获取相关信息:行驶160海里轮船用时8小时,快艇用时4小时;快艇比轮船晚2小时出发.
(1)根据图象过特殊点,用待定系数法分别求关系式;
(2)由函数图象提供的数据信息根据行程问题的数量关系:速度=路程÷时间就可以得出结论;
(3)根据题意列出方程,解方程即可求得.
解答 解:(1)设快艇行驶过程中路程和时间x的函数关系式为y=k1x,
∵点(8,160)在函数y=k1x的图象上,
∴160=8k1,解得k1=20,
∴快艇行驶过程中路程和时间x的函数关系式为y=20x;
设轮船行驶过程中路程y(千米)和时间x(小时)的函数关系式为y=k2x+b,
∵点(0,40)和(8,120)在此函数的图象上,
∴$\left\{\begin{array}{l}{b=40}\\{8{k}_{2}+b=120}\end{array}\right.$,解得$\left\{\begin{array}{l}{{k}_{2}=10}\\{b=40}\end{array}\right.$,
∴轮船行驶过程中路程y(千米)和时间x(小时)的函数关系式为y=10x+40;,
(2)由图象可知,快艇在8小时内行驶了160千米,
所以它的速度为160÷8=20(千米/小时),
轮船在8小时内行驶了120-40=80(千米),
所以轮船的速度为80÷8=10(千米/小时);
(3)设快艇出发x小时追上轮船,
根据题意得,10x+40=20x,
解得x=4,
所以快艇出发4小时追上轮船.
点评 本题考查了一次函数的图象的运用,行程问题的数量关系的运用,解答时分析清楚函数图象提供的信息是关键.

练习册系列答案
相关题目
5.教室里的饮水机接通电源就进入自动程序,开机加热时水温上升,加热到100℃停止加热,水温开始下降,水温降至30℃,饮水机自动开始加热,重复上述程序.值日生小明7点钟到校后接通饮水机电源,在水温下降的过程中进行了水温检测,记录如下表:
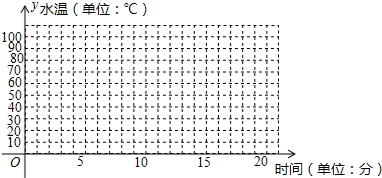
(1)在图中的平面直角坐标系,画出水温y关于饮水机接通电源时间x的函数图象;
(2)借助(1)所画的图象,判断从7:00开始加温到水温第一次降到30℃为止,水温y和时间x之间存在怎样的函数关系?试求出函数关系并写出自变量x取值范围;
(3)上午第一节下课时间为8:25,同学们能不能喝到不超过50℃的水?请通过计算说明.
| 时间x | 7:00 | 7:02 | 7:05 | 7:07 | 7:10 | 7:14 | 7:20 |
| 水温y | 30℃ | 50℃ | 80℃ | 100℃ | 70℃ | 50℃ | 35℃ |
(2)借助(1)所画的图象,判断从7:00开始加温到水温第一次降到30℃为止,水温y和时间x之间存在怎样的函数关系?试求出函数关系并写出自变量x取值范围;
(3)上午第一节下课时间为8:25,同学们能不能喝到不超过50℃的水?请通过计算说明.

9.下列四个数中,负数是( )
| A. | |-2| | B. | -22 | C. | -(-2) | D. | $\sqrt{(-2)^{2}}$ |
19. 如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )
如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )
 如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )
如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )| A. | b-a>0 | B. | a+b<0 | C. | ab<0 | D. | b<a |
 如图,AD,AE分别是△ABC的高和中线,已知AD=5,CE=4,则△ABC的面积为20.
如图,AD,AE分别是△ABC的高和中线,已知AD=5,CE=4,则△ABC的面积为20.
 如图,己知∠1=∠2,∠3=∠4.求证:AB=CD.
如图,己知∠1=∠2,∠3=∠4.求证:AB=CD.