题目内容
10.(1)计算:(-2)2+|-$\sqrt{3}$|-2sin60°-$\sqrt{8}$;(2)求不等式组$\left\{\begin{array}{l}{2x+1>0}\\{x>2x-5}\end{array}\right.$的正整数解.
分析 (1)直接利用利用绝对值的性质以及特殊角的三角函数值和二次根式的性质化简各数,进而求出答案;
(2)分别解不等式,进而得出不等式组的解集.
解答 解:(1)原式=4+$\sqrt{3}$-$\sqrt{3}$-2$\sqrt{2}$
=4-2$\sqrt{2}$;
(2)$\left\{\begin{array}{l}{2x+1>0①}\\{x>2x-5②}\end{array}\right.$
∵不等式①的解集是:x>-$\frac{1}{2}$,
不等式②的解集是:x<5,
∴原不等式组的解集是:-$\frac{1}{2}$<x<5,
∴原不等式组的正整数解是1,2,3,4.
点评 此题主要考查了实数运算以及不等式组的解法,正确化简各数是解题关键.

练习册系列答案
相关题目
5.直线y=2x+2沿y轴向下平移6个单位后与y轴的交点坐标是( )
| A. | (0,2) | B. | (0,8) | C. | (0,4) | D. | (0,-4) |
15.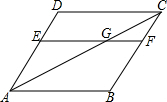 如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有(∠BAC除外)( )
如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有(∠BAC除外)( )
 如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有(∠BAC除外)( )
如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有(∠BAC除外)( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
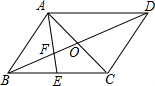 已知:如图,四边形ABCD中,AC与BD交于点O,且OA=OC,AD∥BC
已知:如图,四边形ABCD中,AC与BD交于点O,且OA=OC,AD∥BC
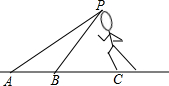 北京时间2008年8月16日晚上22:30,北京奥运会男子百米飞人大战在鸟巢打响,最终博尔特以9秒69的成绩打破世界纪录并轻松夺冠,博尔特再次打破人类历史,A,B两个镜头同时拍下了博尔特冲刺时的画面;从A镜头观测博尔特仰角为21°,从B镜头观测博尔特仰角为37°,已知AB=2.6米,你能根据上述信息计算出博尔特的身高吗?(sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$)
北京时间2008年8月16日晚上22:30,北京奥运会男子百米飞人大战在鸟巢打响,最终博尔特以9秒69的成绩打破世界纪录并轻松夺冠,博尔特再次打破人类历史,A,B两个镜头同时拍下了博尔特冲刺时的画面;从A镜头观测博尔特仰角为21°,从B镜头观测博尔特仰角为37°,已知AB=2.6米,你能根据上述信息计算出博尔特的身高吗?(sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$)