题目内容
1.已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.(Ⅰ)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(Ⅱ)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC,求∠ODC的度数.
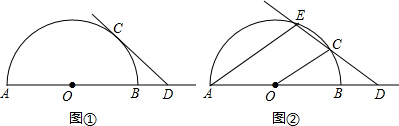
分析 (1)连接OC,因为CD是⊙O的切线,得出∠OCD=90°,由OC=CD,得出∠ODC=∠COD,即可求得.
(2)连接OE,利用等腰三角形及平行线的性质,可求得∠ODC的度数.
解答 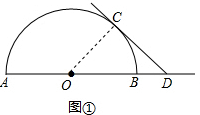 解:(1)如图①,连接OC,
解:(1)如图①,连接OC,
∵OC=OA,CD=OA,
∴OC=CD,
∴∠ODC=∠COD,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ODC=45°;
(2)如图②,连接OE.
∵CD=OA,∴CD=OC=OE=OA,
∴∠1=∠2,∠3=∠4.
∵AE∥OC,
∴∠2=∠3.
设∠ODC=∠1=x,则∠2=∠3=∠4=x.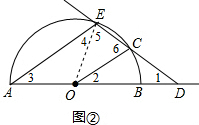
∴∠AOE=∠OCD=180°-2x.
∵∠6=∠1+∠2=2x.
∵OE=OC,∴∠5=∠6=2x.
∵AE∥OC,
∴∠4+∠5+∠6=180°,即:x+2x+2x=180°,
∴x=36°.
∴∠ODC=36°.
点评 本题考查了切线性质,全等三角形,等腰三角形的性质以及平行线的性质等,作出辅助线是解题的关键.

练习册系列答案
相关题目
12.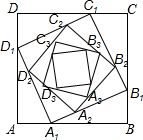 如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
 如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )| A. | $\frac{8}{9}{a}^{2}$ | B. | ($\frac{4}{9}$)na2 | C. | ($\frac{5}{9}$)n-1a2 | D. | ($\frac{5}{9}$)na2 |
9. 如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
 如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )| A. | 40° | B. | 50° | C. | 60° | D. | 30° |
16.我们知道,中式窗户的图案非常多样,美轮美奂,在下面几个比较简单的窗户图案中,可以看作是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.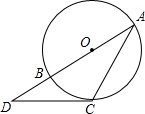 如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )
如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )
 如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )
如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
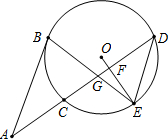 如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为$\widehat{DC}$的中点,连接OE交CD于点F,连接BE交CD于点G.
如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为$\widehat{DC}$的中点,连接OE交CD于点F,连接BE交CD于点G.