题目内容
20.(1)解方程:$\frac{3x}{x-2}$-1=$\frac{2}{2-x}$(2)解不等式组$\left\{\begin{array}{l}{2-x≤0}\\{2x-3<\frac{1}{2}(x+3)}\end{array}\right.$.
分析 (1)按照解分式方程的步骤,即可解答;
(2)按照解一元一次不等式组的步骤,即可解答.
解答 解:(1)方程两边同乘(x-2)得:3x-(x-2)=-2,
解得:x=-2,
当x=-2时,x-2≠0,
∴方程方程的解为:x=-2;
(2)$\left\{\begin{array}{l}{2-x≤0①}\\{2x-3<\frac{1}{2}(x+3)②}\end{array}\right.$
由①得:x≥2,
由②得:x<3,
∴不等式组的解为:2≤x<3.
点评 本题考查了解分式方程、解一元一次不等式组,解决本题的关键是熟记解分式方程、解一元一次不等式组的步骤.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )
如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )
 如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )
如图,在?ABCD中,点E在DC上,BE与AC相交于点F,若$\frac{DE}{EC}$=$\frac{1}{2}$,则$\frac{BF}{BE}$的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
15.某同学一周中每天体育运动所花时间(单位:分钟)分别为:35,40,45,40,55,40,48,这组数据的中位数是( )
| A. | 35 | B. | 40 | C. | 45 | D. | 55 |
12.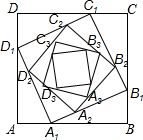 如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
 如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )| A. | $\frac{8}{9}{a}^{2}$ | B. | ($\frac{4}{9}$)na2 | C. | ($\frac{5}{9}$)n-1a2 | D. | ($\frac{5}{9}$)na2 |
9. 如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
 如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )
如图,直线AB∥CD,∠1=50°,∠2=110°,则∠E的大小是( )| A. | 40° | B. | 50° | C. | 60° | D. | 30° |
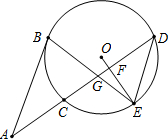 如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为$\widehat{DC}$的中点,连接OE交CD于点F,连接BE交CD于点G.
如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为$\widehat{DC}$的中点,连接OE交CD于点F,连接BE交CD于点G.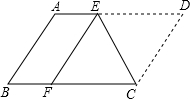 如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AB上.
如图,将?ABCD沿CE折叠,使点D落在BC边上的F处,点E在AB上.