Question

19．已知：正方形ABCD的边长为4cm，点E从点A出发沿AD方向以1cm/秒的速度运动，与此同时，点F也从点D出发沿DC方向相同的速度运动，记运动的时间为t（0≤t≤4），AF与BE交于P点．
（1）如图，在运动过程中，AF与BE相等吗？请说明理由．
（2）在运动过程中，要使得△BPC是等腰三角形，t应为何值？请画出图形，并求出所有满足条件的t值．

Answer 1

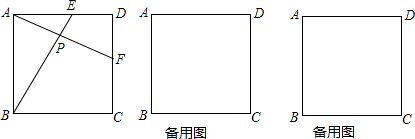
分析 （1）结论：AF=BE，只要证明△ABE≌△DAF即可．
（2）分两种情形讨论：①如图2中，当CP=CB时，作CM⊥BE垂足为O，交AB于M，先证明AM=BM，再证明△ABE≌△CBM即可，②如图3中，当点E运动到与点D重合，点F运动到与点C重合时，△PBC是等腰三角形，求出t即可．

解答 （1）结论：AF=BE，
证明：如图1中，∵四边形ABCD是正方形，
∴AB=AD，∠BAE=∠D=90°，
在△ABE和△DAF中，
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠D}\\{AE=DF}\end{array}\right.$，
∴△ABE≌△DAF，
∴BE=AF．
（2）①如图2中，当CP=CB时，作CM⊥BE垂足为O，交AB于M．
∵△ABE≌△DAF，
∴∠ABE=∠DAF，
∵∠ABE+∠AEB=90°，
∴∠DAF+∠AEB=90°
∴∠APE=90°，
∴AF⊥BE，
∴OM∥AP，
∵OP=OB，
∴AM=BM，
∵∠ABE+∠AEB=90°∠ABE+∠CMB=90°，
∴∠AEB=∠CMB，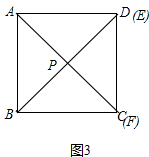
在△ABE和△CBM中，
$\left\{\begin{array}{l}{∠BAE=∠CBM=90°}\\{∠AEB=∠CMB}\\{AB=BC}\end{array}\right.$，
∴△ABE≌△CBM，
∴AE=BM=2，
∴t=2，
②如图3中，当点E运动到与点D重合，点F运动到与点C重合时，△PBC是等腰三角形，此时t=4，
③当t=0时，点E在点A处，点F在点D处，则AF于BE的交点P于点A重合，此时，△BPC显然是等腰直角三角形
∴t=0或2或4时，△BPC是等腰三角形．

点评 本题考查正方形的性质、等腰三角形的性质、全等三角形的判定和性质等知识，解题的关键是学会分类讨论，正确画出图形，属于中考常考题型．