题目内容
2.甲、乙、丙三位同学在操场上互相传球,假设他们相互间传球是等可能的,并且由甲首先开始传球.(1)经过2次传球后,球仍回到甲手中的概率是$\frac{1}{2}$;
(2)请用列举法(画树状图或列表)求经过3次传球后,球仍回到甲手中的概率;
(3)猜想并直接写出结论:经过n次传球后,球传到甲、乙这两位同学手中的概率:P(球传到甲手中)和P(球传到乙手中)的大小关系.
分析 (1)画树状图展示所有4种等可能的结果数,再找出球仍回到甲手中的结果数,然后根据概率公式求解;
(2)画树状图展示所有8种等可能的结果数,再找出球仍回到甲手中的结果数,然后根据概率公式求解;
(3)利用(1)、(2)的结论讨论:当n为偶数时,P(球传到甲手中)>P(球传到乙手中)的大小关系;当n为奇数时,P(球传到甲手中)<P(球传到乙手中)的大小关系.
解答 解:(1)画树状图为:
共有4种等可能的结果数,其中球仍回到甲手中的结果数为2,
所以球仍回到甲手中的概率=$\frac{2}{4}$=$\frac{1}{2}$;
故答案为$\frac{1}{2}$;
(2)画树状图为:
共有8种等可能的结果数,其中球仍回到甲手中的结果数为2,
所以球仍回到甲手中的概率=$\frac{2}{8}$=$\frac{1}{4}$;
(3)当n为偶数时,P(球传到甲手中)>P(球传到乙手中)的大小关系;
当n为奇数时,P(球传到甲手中)<P(球传到乙手中)的大小关系.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
12.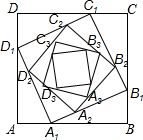 如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
 如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=$\frac{1}{3}$a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=$\frac{1}{3}$A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )| A. | $\frac{8}{9}{a}^{2}$ | B. | ($\frac{4}{9}$)na2 | C. | ($\frac{5}{9}$)n-1a2 | D. | ($\frac{5}{9}$)na2 |
14.一组数据6,x,8,10,16的平均数为10,则这组数据的众数、中位数分别是( )
| A. | 10,16 | B. | 8,10 | C. | 10,12 | D. | 10,10 |
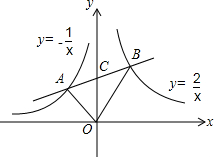 如图,已知直线AB与反比例函数$y=-\frac{1}{x}$和$y=\frac{2}{x}$交于A、B两点,与y轴交于点C,若AC=BC,则S△AOB=$\frac{3}{2}$.
如图,已知直线AB与反比例函数$y=-\frac{1}{x}$和$y=\frac{2}{x}$交于A、B两点,与y轴交于点C,若AC=BC,则S△AOB=$\frac{3}{2}$.