题目内容
18．
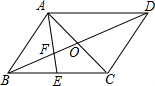已知：如图，四边形ABCD中，AC与BD交于点O，且OA=OC，AD∥BC（1）求证：AD=CB；
（2）若E是BC的中点，连接AE交BD于F，求$\frac{AF}{EF}$的值．
分析 （1）由AD∥BC，得到∠DAO=∠BCO，根据ASA即可判断．
（2）由AD∥BE得到$\frac{AF}{EF}$=$\frac{AD}{BE}$即可解决问题．
解答 （1）证明：∵AD∥BC，
∴∠DAO=∠BCO，
在△ADO和△CBO中，
$\left\{\begin{array}{l}{∠DAO=∠BCO}\\{∠AOD=∠BOC}\\{AO=OC}\end{array}\right.$，
∴△ADO≌△CBO，
∴AD=BC．
（2）∵AD∥BC，AD=BC，BE=EC，
∴AD=2BE，
∴$\frac{AD}{BE}$=$\frac{AF}{FE}$=$\frac{2}{1}$，
∴$\frac{AF}{FE}$=2．
点评 本题考查全等三角形的判定和性质、平行线分线段成比例定理等知识，解题的关键是熟练掌握全等三角形的判定和性质，学会应用平行线分线段成比例定理，属于中考常考题型．
练习册系列答案
相关题目
9．
如图，直线AB∥CD，∠1=50°，∠2=110°，则∠E的大小是（ ）
如图，直线AB∥CD，∠1=50°，∠2=110°，则∠E的大小是（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 30° |
6．
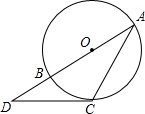如图，⊙O的直径AB=2，点D在AB的延长线上，DC与⊙O相切于点C，连接AC．若∠A=30°，则CD长为（ ）
如图，⊙O的直径AB=2，点D在AB的延长线上，DC与⊙O相切于点C，连接AC．若∠A=30°，则CD长为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{2\sqrt{3}}}{3}$ | D． | $\sqrt{3}$ |
3．在Rt△ABC中，∠C=90°，sinA=$\frac{3}{5}$，b=4，则tanB=（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{5}{4}$ |