题目内容
20.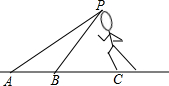 北京时间2008年8月16日晚上22:30,北京奥运会男子百米飞人大战在鸟巢打响,最终博尔特以9秒69的成绩打破世界纪录并轻松夺冠,博尔特再次打破人类历史,A,B两个镜头同时拍下了博尔特冲刺时的画面;从A镜头观测博尔特仰角为21°,从B镜头观测博尔特仰角为37°,已知AB=2.6米,你能根据上述信息计算出博尔特的身高吗?(sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$)
北京时间2008年8月16日晚上22:30,北京奥运会男子百米飞人大战在鸟巢打响,最终博尔特以9秒69的成绩打破世界纪录并轻松夺冠,博尔特再次打破人类历史,A,B两个镜头同时拍下了博尔特冲刺时的画面;从A镜头观测博尔特仰角为21°,从B镜头观测博尔特仰角为37°,已知AB=2.6米,你能根据上述信息计算出博尔特的身高吗?(sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$)
分析 此题可作PC⊥AB,利用两仰角的正切值及PC的长表示AB,即AB=$\frac{PC}{tan21°}$-$\frac{PC}{tan37°}$,求得PC即可.
解答  解:作PC⊥AB,
解:作PC⊥AB,
设PC=x,∠PBC=37°,则CB=$\frac{x}{tan37°}$,
∵∠PAC=21°,
∴AC=$\frac{x}{tan21°}$,
∴$\frac{x}{tan21°}$-$\frac{x}{tan37°}$=2.6,即$\frac{x}{\frac{3}{8}}$-$\frac{x}{\frac{3}{4}}$=2.6,
解得x=1.95.
答:博尔特的身高约为1.95米.
点评 本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
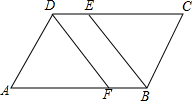 已知,如图,在?ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,求证:BF=DE.
已知,如图,在?ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,求证:BF=DE.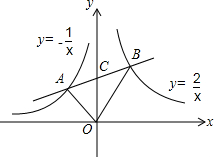 如图,已知直线AB与反比例函数$y=-\frac{1}{x}$和$y=\frac{2}{x}$交于A、B两点,与y轴交于点C,若AC=BC,则S△AOB=$\frac{3}{2}$.
如图,已知直线AB与反比例函数$y=-\frac{1}{x}$和$y=\frac{2}{x}$交于A、B两点,与y轴交于点C,若AC=BC,则S△AOB=$\frac{3}{2}$. 如图所示,OA垂直平分PM,OB垂直平分PN,且MN交OA,OB于C,D,MN=8cm,则△PCD的周长为8cm.
如图所示,OA垂直平分PM,OB垂直平分PN,且MN交OA,OB于C,D,MN=8cm,则△PCD的周长为8cm.