题目内容
7．
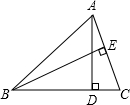如图，在△ABC中，AD、BE分别是BC、AC上的高，BC=9，AC=6．求：（1）AD：BE的值；
（2）若BE=8，求AD的长．
分析 （1）根据三角形的面积公式得出$\frac{1}{2}$BC•AD=$\frac{1}{2}$AC•BE，再把AC和BC的值代入即可得出△ABC的高AD与BE的比；
（2）根据（1）的结论代入BE=8，即可得到结论．
解答 解：（1）∵S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$AC•BE，AC=6，BC=9，
∴$\frac{1}{2}$×9•AD=$\frac{1}{2}$×6•BE，
∴3AD=2BE，
∴$\frac{AD}{BE}$=$\frac{2}{3}$；
（2）由（1）得$\frac{AD}{BE}$=$\frac{2}{3}$，
∵BE=8，
∴AD=$\frac{16}{3}$．
点评 此题考查了比例线段和三角形的面积，利用两个底边和对应的高线列出面积的表达式是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
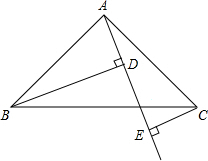如图，Rt△ABC中，AB=AC，∠BAC=90°，直线AE是经过点A的任一直线，BD⊥AE于D，CE⊥AE于E，若BD＞CE，试解答：
如图，已知直线l和A，B两点，求作经过A，B两点的圆，使圆心在直线l上．
一辆汽车和一辆摩托车同时分别从A，B两地去同一城市，它们离A地的路程随时间变化的图象如图所示．当汽车到达目的地时，摩托车距目的地20千米．
如图，B，C分别在△ADE的边AD，AE上，且AC=6，AB=5，EC=4，DB=7，则BC：DE=$\frac{1}{2}$．
如图，直角三角形两直角边的长分别是2、3，阴影部分是一个正方形，设正方形的边长为a，