题目内容
17.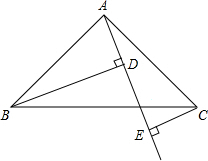 如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试解答:
如图,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试解答:(1)AD与CE的大小关系如何?请说明理由.
(2)若BD=5,CE=2,求DE的长.
分析 (1)根据全等三角形的判定与性质,可得答案;
(2)根据全等三角形的性质,可得AD、AD的长,根据线段的和差,可得答案.
解答 解:(1)AD=CE,
∵∠BAC=90°,BD⊥AE,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠ADB=∠CEA}\\{AB=CA}\end{array}\right.$,
∴△ABD≌△CAE (AAS),
∴AD=CE.
(2)∵△ABD≌△CAE,
∴BD=AE=5,AD=CE=2,
∴DE=AE-AD=BD-CE=5-2=3.
点评 本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,利用余角的性质得出∠ABD=∠CAE是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.一家鞋店在一段时间内销售了某种男鞋200双,各种尺码鞋的销售量如表所示:
一般来讲鞋店老板比较关心哪种尺码的鞋最畅销,也就是关心卖出的鞋的尺码组成的一组数据( )
| 尺码/厘米 | 23 | 23.5 | 24 | 24.5 | 25 | 25.5 |
| 销售量/双 | 5 | 10 | 22 | 39 | 56 | 43 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 加权平均数 |
 方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(3,4)、B(-4,3)、C(3,-2).
方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(3,4)、B(-4,3)、C(3,-2).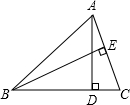 如图,在△ABC中,AD、BE分别是BC、AC上的高,BC=9,AC=6.求:
如图,在△ABC中,AD、BE分别是BC、AC上的高,BC=9,AC=6.求: