题目内容
2. 如图,B,C分别在△ADE的边AD,AE上,且AC=6,AB=5,EC=4,DB=7,则BC:DE=$\frac{1}{2}$.
如图,B,C分别在△ADE的边AD,AE上,且AC=6,AB=5,EC=4,DB=7,则BC:DE=$\frac{1}{2}$.
分析 根据已知条件得到$\frac{AC}{AD}=\frac{AB}{AE}$,由∠A=∠A,推出△ABC∽△AED,根据相似三角形的性质即可得到结论.
解答 解:∵AC=6,AB=5,EC=4,DB=7,
∴AE=10,AD=12,
∵$\frac{AC}{AD}=\frac{6}{12}$=$\frac{1}{2}$,$\frac{AB}{AE}$=$\frac{5}{10}=\frac{1}{2}$,
∴$\frac{AC}{AD}=\frac{AB}{AE}$,
∵∠A=∠A,
∴△ABC∽△AED,
∴BC:DE=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
13.根据下列条件,A,B,C三点能确定一个圆的是( )
| A. | AB=2,BC=2,AC=4 | B. | AB=4.5,BC=5.5,AC=10 | ||
| C. | AB=4,BC=3,AC=5 | D. | AB=$\sqrt{2}$-1,BC=$\sqrt{2}$+1,AC=2$\sqrt{2}$ |
10.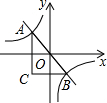 如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx(k<0)的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为( )
如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx(k<0)的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为( )
 如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx(k<0)的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为( )
如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx(k<0)的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为( )| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
12.(1)填表:
(2)由上表找规律,并根据规律填空:
①已知:$\sqrt{49}$=7,则$\sqrt{0.49}$=0.7,$\sqrt{490000}$=700
②已知:$\sqrt{529}$=23,则$\sqrt{0.0529}$=0.23,$\sqrt{52900}$=230.
| a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| $\sqrt{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
①已知:$\sqrt{49}$=7,则$\sqrt{0.49}$=0.7,$\sqrt{490000}$=700
②已知:$\sqrt{529}$=23,则$\sqrt{0.0529}$=0.23,$\sqrt{52900}$=230.
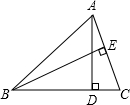 如图,在△ABC中,AD、BE分别是BC、AC上的高,BC=9,AC=6.求:
如图,在△ABC中,AD、BE分别是BC、AC上的高,BC=9,AC=6.求: 已知有理数a、b、c在数轴上的位置如图所示,请标出-a,-b,-c的位置,并用“<“连接这6个数.
已知有理数a、b、c在数轴上的位置如图所示,请标出-a,-b,-c的位置,并用“<“连接这6个数.