题目内容
19.如图1所示,在△ABC中,AD是角平分线,AE是高.(1)若∠B<∠C,试探究∠DAE与$\frac{1}{2}$(∠C-∠B)之间的大小关系,并说明理由.
(2)若将点A移动到点A′,A′E⊥BC于点E,此时∠DAE变为∠DA′E,如图2,直接写出(1)中的结论是否还成立.

分析 (1)根据直角三角形两锐角互余得出∠CAE+∠C=90°,再根据角平分线定义得出∠CAD=∠BAD,然后根据∠DAE=∠CAD-∠CAE进行计算即可得解;
(2)利用三角形的外角等于与它不相邻的两个内角之和先用∠B和∠C表示出∠A′DE,再根据三角形的内角和定理可证明∠DA′E=$\frac{1}{2}$(∠C-∠B).
解答 解:(1)∠DAE=$\frac{1}{2}$(∠C-∠B)
理由:∵AE⊥BC,
∴∠CAE=90°-∠C,
∵AD是△ABC的角平分线,
∴∠CAD=$\frac{1}{2}$∠BAC,
∴∠DAE=∠CAD-∠CAE=$\frac{1}{2}$∠BAC-(90°-∠C)=$\frac{1}{2}$-90°+∠C=$\frac{1}{2}$(∠C-∠B);
(2)∠DA′E=$\frac{1}{2}$(∠C-∠B),
∵∠A′DE=∠B+∠BAD
=∠B+$\frac{1}{2}$∠BAC
=∠B+$\frac{1}{2}$(180°-∠B-∠C)
=90°+$\frac{1}{2}$∠B-$\frac{1}{2}$∠C,
∴∠DA′E=180°-∠A′ED-∠A′DE
=180°-90°-(90°+$\frac{1}{2}$∠B-$\frac{1}{2}$∠C)
=$\frac{1}{2}$(∠C-∠B).
点评 本题考查了三角形的内角和定理,三角形的角平分线,高线的定义,准确识图,找出各角度之间的关系是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
9.(-x2+3xy-$\frac{1}{2}$y2)-(-$\frac{1}{2}$x2+4xy-$\frac{3}{2}$y2)=-$\frac{1}{2}$x2- 空格的地方被弄污了,空格中应该是( )
| A. | -7xy | B. | 7xy | C. | -xy | D. | xy |
10.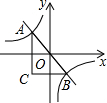 如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx(k<0)的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为( )
如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx(k<0)的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为( )
 如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx(k<0)的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为( )
如图,反比例函数y=-$\frac{4}{x}$的图象与直线y=kx(k<0)的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则△ABC的面积为( )| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
9.若α、β是一元二次方程x2+3x-7=0的两根,则α2+β2=( )
| A. | -7 | B. | 32 | C. | 23 | D. | 14 |
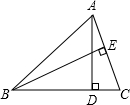 如图,在△ABC中,AD、BE分别是BC、AC上的高,BC=9,AC=6.求:
如图,在△ABC中,AD、BE分别是BC、AC上的高,BC=9,AC=6.求: 已知有理数a、b、c在数轴上的位置如图所示,请标出-a,-b,-c的位置,并用“<“连接这6个数.
已知有理数a、b、c在数轴上的位置如图所示,请标出-a,-b,-c的位置,并用“<“连接这6个数. 如图,在△ABC中,AB=AC,AC的垂直平分线交BC于点D,垂足为E,AB=10cm,且△ABD的周长为23cm.求△ABC的周长.
如图,在△ABC中,AB=AC,AC的垂直平分线交BC于点D,垂足为E,AB=10cm,且△ABD的周长为23cm.求△ABC的周长.