题目内容
18.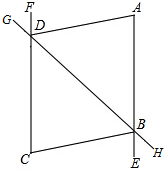 如图,∠GDC+∠HBE=180°,∠DAE=∠BCF,DA平分∠BDF.
如图,∠GDC+∠HBE=180°,∠DAE=∠BCF,DA平分∠BDF.(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)过点D作BC的垂线,垂足为M,求证:∠ABD=2∠CDM.
分析 (1)AE与CF平行,理由为:由邻补角定义及已知两角互补,等量代换得到一对同位角相等,利用同位角相等两直线平行即可得证;
(2)由AE与CF平行,得到一对同旁内角互补,根据∠DAE=∠BCF,等量代换得到另一对同旁内角互补,利用同旁内角互补两直线平行得到AB与CD平行,利用两直线平行同位角相等即可求出所求角的度数;
(3)利用平行线的性质,邻补角的性质,等量代换即可得证.
解答 解:(1)AE∥CF,理由为:
∵∠GDF+∠GDC=180°,∠GDC+∠HBE=180°,
∴∠GDF=∠HBE,
∠ABG=∠HBE,
∴∠GDF=∠ABG,
∴AE∥CF;
(2)∵AE∥CF,
∴∠ABC+∠BCF=180°,
∵∠DAE=∠BCF,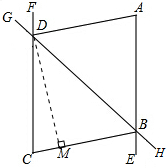
∴∠ABC+∠DAE=180°,
∴AD∥BC;
(3)∵AD∥BC,
∴∠ADF=∠C,
∴∠CDM=90°-∠C=90°-∠ADF,
∵CD∥AB,
∴∠GDF=∠DBA=180°-2∠ADF,
∴∠ABD=2∠CDM.
点评 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
相关题目
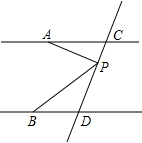 如图,已知AC∥BD,点P是直线CD上的一个动点(P点与点C、D不重合)
如图,已知AC∥BD,点P是直线CD上的一个动点(P点与点C、D不重合)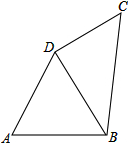 如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32. ①化简:当a≥0时,$\sqrt{{a}^{2}}$=a;当a<0时,$\sqrt{{a}^{2}}$=-a
①化简:当a≥0时,$\sqrt{{a}^{2}}$=a;当a<0时,$\sqrt{{a}^{2}}$=-a