题目内容
6.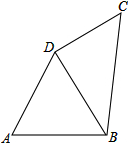 如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.(1)求∠BDC的度数;
(2)四边形ABCD的面积.
分析 (1)先根据题意得出△ABD是等边三角形,△BCD是直角三角形,进而可求出BDC的度数;
(2)根据四边形周长计算BC,CD,即可求△BCD的面积,正△ABD的面积根据计算公式计算,即可求得四边形ABCD的面积为两个三角形的面积的和.
解答 解:(1)∵AB=AD=8cm,∠A=60°,
∴△ABD是等边三角形,
∵∠ADC=150°
∴∠BDC=150°-60°=90°;
(2)∵△ABD为正三角形,AB=8cm,
∴其面积为$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$×AB×AD=16$\sqrt{3}$,
∵BC+CD=32-8-8=16,且BD=8,BD2+CD2=BC2,
解得BC=10,CD=6,
∴直角△BCD的面积=$\frac{1}{2}$×6×8=24,
故四边形ABCD的面积为24+16$\sqrt{3}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
16.点A(4,3)经过平移后得点B(6,-3),它的平移过程是( )
| A. | 向右平移2个单位后再向下平移6个单位 | |
| B. | 向左平移2个单位后再向下平移2个单位 | |
| C. | 向左平移2个单位后再向上平移6个单位 | |
| D. | 向右平移6个单位后再向上平移2个单位 |
17.计算:(-2)2015•($\frac{1}{2}$)2014等于( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
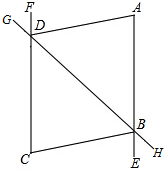 如图,∠GDC+∠HBE=180°,∠DAE=∠BCF,DA平分∠BDF.
如图,∠GDC+∠HBE=180°,∠DAE=∠BCF,DA平分∠BDF.