题目内容
8.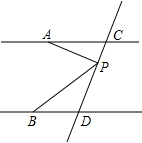 如图,已知AC∥BD,点P是直线CD上的一个动点(P点与点C、D不重合)
如图,已知AC∥BD,点P是直线CD上的一个动点(P点与点C、D不重合)(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD之间有什么关系,这种关系是否发生变化?
(2)若点P在C、D两点的外侧运动时,试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
分析 (1)过点P作PE∥AC,根据平行线的性质得出∠CAP=∠APE,再由PE∥AC,AC∥BD得出PE∥BD,故可得出结论;
(2)当点P在C、D两点的外侧运动时分两种情况进行讨论.
解答  解:(1)如果P点在C、D之间运动时,∠PAC+∠PBD=∠APB,且此关系不变.
解:(1)如果P点在C、D之间运动时,∠PAC+∠PBD=∠APB,且此关系不变.
理由如下:过点P作PE∥AC,则∠CAP=∠APE,
∵PE∥AC,AC∥BD,
∴PE∥BD,
∴∠EPB=∠PBD,
∴∠APB=∠APE+∠EPB=∠PBD+∠CAP;
(2)当点P在C、D两点的外侧运动时,分两种情况:
①当点P在点C上方时,∠PBD=∠PAC+∠APB.
理由如下:如图过点P作PE∥AC,
则∠EPA=∠PAC,∠PBD=∠POC.
∵PE∥AC,AC∥BD,
∴PE∥BD,
∴∠EPB=∠PBD
∴∠PBD=∠POC=∠EPB=∠EPA+∠APB=∠PAC+∠APB.
②同理,当点P在点D下方时,∠PAC=∠PBD+∠APB.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
18.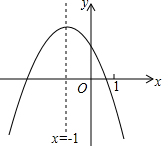 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1),
其中错误的结论是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1),
其中错误的结论是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
16.点A(4,3)经过平移后得点B(6,-3),它的平移过程是( )
| A. | 向右平移2个单位后再向下平移6个单位 | |
| B. | 向左平移2个单位后再向下平移2个单位 | |
| C. | 向左平移2个单位后再向上平移6个单位 | |
| D. | 向右平移6个单位后再向上平移2个单位 |
13. 如图,∠1=∠2,∠B=∠D,下列四个结论中,错误的是( )
如图,∠1=∠2,∠B=∠D,下列四个结论中,错误的是( )
 如图,∠1=∠2,∠B=∠D,下列四个结论中,错误的是( )
如图,∠1=∠2,∠B=∠D,下列四个结论中,错误的是( )| A. | ∠DCA=∠DAC | B. | AD∥BC | C. | AB∥CD | D. | ∠DAC=∠BCA |
17.计算:(-2)2015•($\frac{1}{2}$)2014等于( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
 如图,菱形ABCD中,对角线AC,BD相交于点O,H为AD边的中点,菱形ABCD的边长为12,则OH的长等于( )
如图,菱形ABCD中,对角线AC,BD相交于点O,H为AD边的中点,菱形ABCD的边长为12,则OH的长等于( )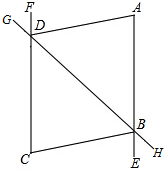 如图,∠GDC+∠HBE=180°,∠DAE=∠BCF,DA平分∠BDF.
如图,∠GDC+∠HBE=180°,∠DAE=∠BCF,DA平分∠BDF.