题目内容
3.计算或解方程:(1)(a-$\sqrt{3}$)(a+$\sqrt{3}$)-a(a-6)
(2)(a-b+$\frac{4ab}{a-b}$)(a+b-$\frac{4ab}{a+b}$)
(3)$\frac{7-9x}{2-3x}$+$\frac{4x-5}{3x-2}$=1
(4)$\frac{2}{x+3}$+$\frac{3}{2}$=$\frac{1}{2x+6}$.
分析 (1)原式利用平方差公式,以及单项式乘以多项式法则计算,去括号合并即可得到结果;
(2)原式括号中两项通分并利用同分母分式的加减法则计算,约分即可得到结果;
(3)分式方程变形后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(4)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=a2-3-a2+6a=6a-3;
(2)原式=$\frac{(a-b)^{2}+4ab}{a-b}$•$\frac{(a+b)^{2}-4ab}{a+b}$=$\frac{(a+b)^{2}(a-b)^{2}}{(a+b)(a-b)}$=(a+b)(a-b)=a2-b2;
(3)方程整理得:$\frac{9x-7}{3x-2}$+$\frac{4x-5}{3x-2}$=1,
去分母得:9x-7+4x-5=3x-2,
移项合并得:10x=10,
解得:x=1,
经检验x=1是分式方程的解;
(4)去分母得:4+3x+9=1,
解得:x=-4,
经检验x=-4是分式方程的解.
点评 此题考查了分式的混合运算,以及解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13. 如图,∠1=∠2,∠B=∠D,下列四个结论中,错误的是( )
如图,∠1=∠2,∠B=∠D,下列四个结论中,错误的是( )
 如图,∠1=∠2,∠B=∠D,下列四个结论中,错误的是( )
如图,∠1=∠2,∠B=∠D,下列四个结论中,错误的是( )| A. | ∠DCA=∠DAC | B. | AD∥BC | C. | AB∥CD | D. | ∠DAC=∠BCA |
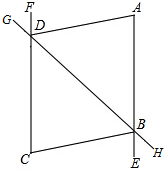 如图,∠GDC+∠HBE=180°,∠DAE=∠BCF,DA平分∠BDF.
如图,∠GDC+∠HBE=180°,∠DAE=∠BCF,DA平分∠BDF.