题目内容
11.在Rt△ABC中,斜边AB=205,$\frac{AC}{BC}$=$\frac{9}{40}$,试求AC,BC的值.分析 可设AC=9x,则BC=40x,在Rt△ABC中,根据勾股定理得到关于x的方程,解方程求出x,进一步求出AC,BC的值.
解答 解:设AC=9x,则BC=40x,
在Rt△ABC中,有(9x)2+(40x)2=2052,
解得x=±5(负值舍去),
AC=9x=9×5=45,
BC=40x=40×5=200.
点评 本题考查了勾股定理和方程思想的应用,勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
6.已知线段a=4,b=8,则线段a,b的比例中项为( )
| A. | ±32 | B. | 32 | C. | $±4\sqrt{2}$ | D. | $4\sqrt{2}$ |
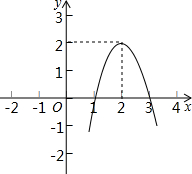 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题: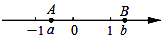 有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$+$\frac{|b-a|}{a-b}$-$\frac{1-b}{|1-b|}$的值是( )
有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$+$\frac{|b-a|}{a-b}$-$\frac{1-b}{|1-b|}$的值是( ) 如图,点E、F在BC上,∠A=∠D,AB=DC,∠B=∠C.求证:BE=FC.
如图,点E、F在BC上,∠A=∠D,AB=DC,∠B=∠C.求证:BE=FC.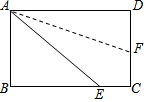 如图,矩形ABCD沿AF折叠,使点D落在BC边上,如果∠BAE=50°,则∠DAF=20°..
如图,矩形ABCD沿AF折叠,使点D落在BC边上,如果∠BAE=50°,则∠DAF=20°..