题目内容
17.先化简,再求值:(a-$\frac{2ab-{b}^{2}}{a}$)÷$\frac{{a}^{2}-{b}^{2}}{a}$,其中a=2+$\sqrt{3}$,b=2-$\sqrt{3}$.分析 先通过通分、化除法为乘法、约分进行化简,然后代入求值.
解答 解:原式=$\frac{(a-b)^{2}}{a}$×$\frac{a}{(a+b)(a-b)}$=$\frac{a-b}{a+b}$.
∵a=2+$\sqrt{3}$,b=2-$\sqrt{3}$,
∴a+b=4,a-b=2$\sqrt{3}$,
∴将其代入,得原式=$\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查了分式的化简求值.分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.就本节内容而言,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
相关题目
8.已知$\frac{a}{b}=\frac{5}{13}$,则$\frac{a-b}{a+b}$的值是( )
| A. | $-\frac{2}{3}$ | B. | $-\frac{3}{2}$ | C. | $-\frac{9}{4}$ | D. | $-\frac{4}{9}$ |
5.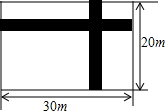 如图,在宽为20米,长为30米的矩形地面上修建两条同样宽为x米的道路,余下部分作为耕地,则耕地面积表示为( )
如图,在宽为20米,长为30米的矩形地面上修建两条同样宽为x米的道路,余下部分作为耕地,则耕地面积表示为( )
 如图,在宽为20米,长为30米的矩形地面上修建两条同样宽为x米的道路,余下部分作为耕地,则耕地面积表示为( )
如图,在宽为20米,长为30米的矩形地面上修建两条同样宽为x米的道路,余下部分作为耕地,则耕地面积表示为( )| A. | (30-x)(20-x)-x2 | B. | (30-x)(20-x) | C. | (30-2x)(20-2x) | D. | (30-2x)(20-x) |
12.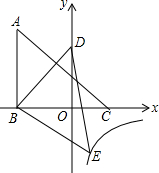 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -3 | B. | -4 | C. | -5 | D. | -3$\sqrt{2}$ |
2.下列运算中,计算正确的是( )
| A. | a3•a2=a6 | B. | a8÷a2=a4 | C. | (ab2)2=a5 | D. | (a2)3=a6 |
9.设二次函数y=ax2+bx+c(a≠0),当x=2时,函数值y=0,则方程ax2+bx+c=0的判别式△=b2-4ac必定是( )
| A. | △=0 | B. | △<0 | C. | △>0 | D. | △≥0 |
6.使分式$\frac{3}{x-2}$有意义的x的取值范围是( )
| A. | x≠2 | B. | x>2 | C. | x<2 | D. | x≥2 |
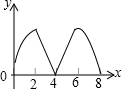
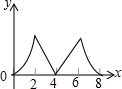
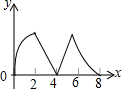
 如图,正方形ABCD边长为4个单位,两动点P、Q分别从点A、B处,以1单位/s、2单位/s的速度逆时针沿边移动.记移动的时间为x(s),△PBQ面积为y(平方单位),当点Q移动一周又回到点B终止,则y与x的函数关系图象为( )
如图,正方形ABCD边长为4个单位,两动点P、Q分别从点A、B处,以1单位/s、2单位/s的速度逆时针沿边移动.记移动的时间为x(s),△PBQ面积为y(平方单位),当点Q移动一周又回到点B终止,则y与x的函数关系图象为( )