题目内容
7.(1)你发现了吗?($\frac{2}{3}$)2=$\frac{2}{3}$×$\frac{2}{3}$,($\frac{2}{3}$)-2=$\frac{1}{(\frac{2}{3})^{2}}$=$\frac{1}{\frac{2}{3}}$×$\frac{1}{\frac{2}{3}}$=$\frac{3}{2}$×$\frac{3}{2}$由上述计算,我们发现($\frac{2}{3}$)2=($\frac{3}{2}$)-2;(2)仿照(1),请你通过计算,判断($\frac{5}{4}$)3与($\frac{4}{5}$)-3之间的关系.
(3)我们可以发现:($\frac{b}{a}$)-m=($\frac{a}{b}$)m(ab≠0)
(4)计算:($\frac{3}{8}$)-4×($\frac{3}{4}$)4.
分析 (1)类比题干中乘方的运算即可得;
(2)类比题干中分数的乘方计算方法计算后即可得;
(3)根据(1)、(2)的规律即可得;
(4)逆用积的乘方将原式变形为($\frac{1}{2}$)-4×($\frac{3}{4}$)-4×($\frac{3}{4}$)4,再利用同底数幂进行计算可得.
解答 解:(1)∵($\frac{2}{3}$)2=$\frac{2}{3}$×$\frac{2}{3}$,($\frac{3}{2}$)-2=$\frac{1}{(\frac{3}{2})^{2}}$=$\frac{1}{\frac{3}{2}×\frac{3}{2}}$=$\frac{2}{3}$×$\frac{2}{3}$,
∴($\frac{2}{3}$)2=($\frac{3}{2}$)-2,
故答案为:=;
(2)∵($\frac{5}{4}$)3=$\frac{5}{4}$×$\frac{5}{4}$×$\frac{5}{4}$,($\frac{4}{5}$)-3=$\frac{1}{\frac{4}{5}×\frac{4}{5}×\frac{4}{5}}$=$\frac{5}{4}$×$\frac{5}{4}$×$\frac{5}{4}$,
∴($\frac{5}{4}$)3=($\frac{4}{5}$)-3;
(3)由(1)、(2)知,($\frac{b}{a}$)-m=($\frac{a}{b}$)m,
故答案为:=;
(4)原式=($\frac{1}{2}$×$\frac{3}{4}$)-4×($\frac{3}{4}$)4
=($\frac{1}{2}$)-4×($\frac{3}{4}$)-4×($\frac{3}{4}$)4
=$\frac{1}{(\frac{1}{2})^{4}}$×($\frac{3}{4}$)-4+4
=16×1
=16.
点评 本题主要考查有理数的乘方、负整数指数幂及幂的运算,熟练掌握有理数的乘方法则和幂的运算法则是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | m3+m3=m6 | B. | m3•m3=2m3 | C. | (-m)•(-m)4=-m5 | D. | (-m)5÷(-m)2=m3 |
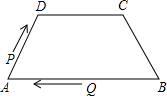 如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.
如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.