题目内容
12.若一元二次方程ax2=b(ab>0)的两根分别为m+1与2m-4.(1)求m的值;
(2)求$\frac{b}{a}$的值.
分析 (1)求出方程ax2=b的根,得出方程m+1+2m-4=0,求出即可;
(2)根据(1)中求出的x=$±\sqrt{\frac{b}{a}}$得出$\frac{b}{a}$=(±2)2,求出即可.
解答 解:(1)ax2=b,
x2=$\frac{b}{a}$,
x=$±\sqrt{\frac{b}{a}}$,
即方程的两根互为相反数,
∵一元二次方程ax2=b(ab>0)的两根分别为m+1与2m-4.
∴m+1+2m-4=0,
解得:m=1;
(2)当m=1时,m+1=2,2m-4=-2,
∵x=±$\frac{b}{a}$,一元二次方程ax2=b(ab>0)的两根分别为m+1与2m-4,
∴$\frac{b}{a}$=(±2)2=4.
点评 本题考查了解一元二次方程和相反数,能求出关于m的方程是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.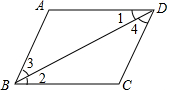 如图所示,下列判断中错误的是( )
如图所示,下列判断中错误的是( )
 如图所示,下列判断中错误的是( )
如图所示,下列判断中错误的是( )| A. | 因为AD∥BC,所以∠3=∠4 | B. | 因为AB∥CD,所以∠ABC+∠C=180° | ||
| C. | 因为∠1=∠2,所以AD∥BC | D. | 因为∠A+∠ADC=180°,所以AB∥CD |
17.某公司有A、B两种客车,它们的载客量和租金如下表,星星中学根据实际情况,计划用A、B型车共5辆,同时送七年级师生到校基地参加社会实践活动.
(1)若要保证租金费用不超过980元,请问该学校有哪几种租车方案?
(2)在(1)的条件下,若七年级师生共有150人,问哪种租车方案最省钱?
| A | B | |
| 载客量(人/辆) | 40 | 20 |
| 租金(元/辆) | 200 | 150 |
(2)在(1)的条件下,若七年级师生共有150人,问哪种租车方案最省钱?