题目内容
19.观察下列运算①由($\sqrt{2}+1$)($\sqrt{2}-1$)=1,得$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}-1$;
②由($\sqrt{3}+\sqrt{2}$)($\sqrt{3}-\sqrt{2}$)=1,得$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}-\sqrt{2}$;
③由($\sqrt{4}$$+\sqrt{3}$)($\sqrt{4}$$-\sqrt{3}$)=1,得$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\sqrt{4}$$-\sqrt{3}$;
④由($\sqrt{5}$$+\sqrt{4}$)($\sqrt{5}$$-\sqrt{4}$)=1,得$\frac{1}{\sqrt{5}+\sqrt{4}}$=$\sqrt{5}$$-\sqrt{4}$;
…
(1)通过观察,将你发现的规律用含有n的式子表示出来.
(2)利用你发现的规律,计算:$\frac{1}{\sqrt{2}+1}$$+\frac{1}{\sqrt{3}+\sqrt{2}}$$+\frac{1}{\sqrt{4}+\sqrt{3}}$$+\frac{1}{\sqrt{5}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2017}+\sqrt{2016}}$.
分析 (1)原式仿照阅读材料中的方法:结果与分母只差一个符号,根据此规律求出值即可;
(2)原式第一个括号中仿照阅读材料中的方法变形,计算即可得到结果.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}-\sqrt{n}$(n为正整数);
(2)原式=($\sqrt{2}$-1)+($\sqrt{3}$-$\sqrt{2}$)+($\sqrt{4}-\sqrt{3}$)+…+($\sqrt{2017}-\sqrt{2016}$),
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2017}-\sqrt{2016}$,
=$\sqrt{2017}$-1.
点评 此题考查了分母有理化,弄清阅读材料中的方法是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列实数中,属于有理数的是( )
| A. | $\sqrt{2}$ | B. | $\root{3}{4}$ | C. | π | D. | $\frac{1}{11}$ |
10.下列运算正确的是( )
| A. | a3•a2=a6 | B. | (a2)3=a5 | C. | (-3a2)3=-9a6 | D. | a2•(-2a)3=-8a5 |
14.某乒乓球馆有两种计费方案,如下图表.李强和同学们打算周末去此乒乓球馆连续打球4小时,经服务生测算后,告知他们包场计费方案会比人数计费方案便宜,则他们参与包场的人数至少为( )
| 包场计费:包场每场每小时50元,每人须另付入场费5元 |
| 人数计费:每人打球2小时20元,接着续打球每人每小时6元 |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
11.某商人将单价为8元的商品按每件10元出售,每天可销售100件,已知这种商品每提高2元,其销量就要减少10件,为了使每天所赚利润最多,该商人应将销售价(为偶数)提高( )
| A. | 8元或10元 | B. | 12元 | C. | 8元 | D. | 10元 |
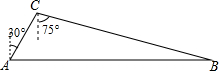 如图,油库C位于油井A北偏东30°方向,输油管道AC的长为50千米,新建油井B位于C南偏东75°方向,且位于A的正东方向.
如图,油库C位于油井A北偏东30°方向,输油管道AC的长为50千米,新建油井B位于C南偏东75°方向,且位于A的正东方向.