题目内容
18.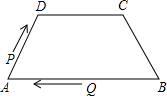 如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.
如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.
分析 首先利用t表示出CP和CQ的长,根据四边形PQBC是平行四边形时CP=BQ,据此列出方程求解即可.
解答 解:设运动时间为t秒,则CP=12-3t,BQ=t,
根据题意得到12-3t=t,
解得:t=3,
故答案为:3.
点评 本题考查了平行四边形的判定及动点问题,解题的关键是化动为静,分别表示出CP和BQ的长,难度不大.

练习册系列答案
相关题目
9.下列实数中,属于有理数的是( )
| A. | $\sqrt{2}$ | B. | $\root{3}{4}$ | C. | π | D. | $\frac{1}{11}$ |
6.下列式子中,y是x的反比例函数的是( )
| A. | y=$\frac{1}{{x}^{2}}$ | B. | y=$\frac{x}{2}$ | C. | y=$\frac{x}{x+1}$ | D. | xy=1 |
3.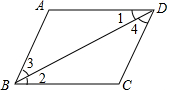 如图所示,下列判断中错误的是( )
如图所示,下列判断中错误的是( )
 如图所示,下列判断中错误的是( )
如图所示,下列判断中错误的是( )| A. | 因为AD∥BC,所以∠3=∠4 | B. | 因为AB∥CD,所以∠ABC+∠C=180° | ||
| C. | 因为∠1=∠2,所以AD∥BC | D. | 因为∠A+∠ADC=180°,所以AB∥CD |
10.下列运算正确的是( )
| A. | a3•a2=a6 | B. | (a2)3=a5 | C. | (-3a2)3=-9a6 | D. | a2•(-2a)3=-8a5 |
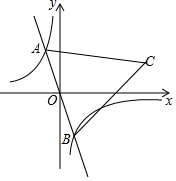 如图,反比例函数y1=$\frac{-2}{x}$的图象有一个动点A,过点A、O作直线y2=ax,交
如图,反比例函数y1=$\frac{-2}{x}$的图象有一个动点A,过点A、O作直线y2=ax,交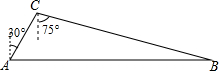 如图,油库C位于油井A北偏东30°方向,输油管道AC的长为50千米,新建油井B位于C南偏东75°方向,且位于A的正东方向.
如图,油库C位于油井A北偏东30°方向,输油管道AC的长为50千米,新建油井B位于C南偏东75°方向,且位于A的正东方向.